
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задача о загрузке оборудованияИмеется m станков, на каждом из которых можно выпускать любые из n деталей. Известно максимально возможное время работы каждого станка: bi , i=1,…, m. Известна длительность изготовления каждой детали на каждом из станков: ai j, i=1,…, m, j=1, …, n, т.е. ai j - длительность обработки j–ой детали, если она изготавливается на i-ом станке. Заданы также затраты на выпуск каждой детали на каждом из станков uij , i=1, …,m, j=1, …, n, и цены, по которым продаются детали: cj , j=1, …,n. Требуется найти, сколько деталей каждого вида следует изготовить на каждом из станков, чтобы получить максимальную прибыль. Обозначим через xij количество деталей j–го вида, которые требуется выпустить на i–ом станке. Тогда a11x11 – время работы 1-го станка над производством 1-ой детали, a12x12 – над производством 2-ой детали и т.д. Общее время работы 1-го станка над запланированной для него программой выпуска деталей составит a11x11+ a12x12+ . . . + a1nx1n. Поскольку время работы 1-го станка ограничено величиной b1, возникает ограничение a11x11+ a12x12+ . . . + a1nx1n≤ b1. Понятно, что аналогичные ограничения возникают для 2-го, 3-го, . . . , m-го станка: ai1xi1+ ai2xi2+ . . . + ainxin≤ bi, i=2,3, . . . ,m. Рассмотрим целевую функцию задачи. Количество деталей j-го вида составит x1j+ x2j+ . . . + xmj штук; cj(x1j+ x2j+ . . . + xmj) – выручка от их продажи. Затраты на производство деталей j-го вида составят u1j x1j + u2j x2j+ . . . + umj xmj. Поэтому прибыль от производства деталей j-го вида, будет определяться формулой
Суммируя по всем видам деталей, получаем целевую функцию задачи:
C учетом неотрицательности искомых переменных математическая модель задачи формулируется следующим образом:
Если также задано условие, что деталей k-го вида необходимо выпустить не менее Sk единиц, то вводится следующее ограничение:  x1k + x2k … + xmk > = Sk. Задача о рационе В рацион для откорма сельскохозяйственных животных должны входить m питательных веществ. Известны величины минимально необходимого потребления каждого из этих веществ: bi, i=1, …, m. Рацион составляется из n видов продуктов. Содержание питательных веществ в единице каждого из продуктов известно: ai j , i=1, …, m, j =1, …, n, где aij – содержание i-го питательного вещества в единице j-го продукта. Известны цены на продукты, которые могут входить в рацион: cj, j=1,…, n. Требуется составить рацион минимальной стоимости, обеспечивающий выполнение всех требований к содержанию питательных веществ. Обозначим через xj количество единиц j-го продукта, которое должно входит в рацион минимальной стоимости. Тогда математическая модель задачи формулируется следующим образом:
Задача о раскрое Для изготовления изделий m типов выполняется раскрой одинаковых заготовок материала. Имеется n способов раскроя. Для каждого способа раскроя известно количество изделий каждого типа, получаемых из одной заготовки: aij, i=1,…,m, j=1,…, n; здесь aij – количество изделий i-го типа, получаемых из одной заготовки при ее раскрое j-м способом. Известны величины отходов для каждого способа раскроя: cj, j=1, … , n. Задано количество изделий каждого типа, которые требуется получить при раскрое: bi, i=1,…,m. Требуется составить оптимальный план раскроя материала, т.е. найти сколько заготовок требуется раскроить каждым из способов, чтобы получить заданное количество изделий при минимальных отходах. Обозначим количество заготовок, раскраиваемых по j–му способу, как xj. Тогда математическая модель задачи формулируется следующим образом:
Задача о смеси Требуется составить смесь, в которою должны входить m компонентов. Заданы нижние (di) и верхние (Di) ограничения на содержание компонентов в смеси, i=1,…,m. Для составления смеси могут использоваться n веществ. Известно содержание каждого компонента в каждом из веществ: aij, i=1,..,m, j=1,...,n; здесь aij- содержание i-го компонента в j-м веществе (в долях или процентах ). Заданы также цены единицы каждого из веществ: cj, j=1,…,n. Требуется определить состав смеси, стоимость которого была бы минимальной. Обозначим через xj содержание j-го вещества в единице смеси. Тогда математическая модель задачи формулируется следующим образом:
Транспортная задача. Имеется m поставщиков однотипной продукции. Каждый из поставщиков обладает запасами в ai единиц этой продукции, i=1,…,m. Эту продукцию потребляют n потребителей. При этом каждый потребитель может использовать bj единиц продукции, j=1,…,n. Доставка единицы продукции от i-го поставщика к j-му потребителю обходится cij денежных единиц. Необходимо составить план доставки продукции от поставщиков к потребителям, который бы обладал минимальными транспортными издержками. Введем в рассмотрение переменные xij — план поставки продукции от i-го поставщика к j-му потребителю. Тогда cijxij - транспортные затраты, связанные с этой поставкой. Общая сумма транспортных затрат будет представлять целевую функцию транспортной задачи:
Рассмотрим вопрос об ограничениях. Во-первых, каждый поставщик обладает ограниченными запасами продукции. Поэтому общая сумма выполняемых им поставок не может превышать имеющихся у него запасов:
Во вторых, необходимо обеспечить потребности каждого потребителя. Сумма поставок от всех поставщиков должна соответствовать его потребностям:
С учетом естественных ограничений (xij≥0) математическая модель задачи принимает вид:
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 396. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
. .
.


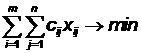 .
.

