
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Игры против природы – наши критерииОсобое место в теории игр занимают игры против природы, которые ещё носят названиевыбора решений при неопределённости. Природа хотя и делает случайные ходы, но не является злонамеренным игроком, так как она не стремится сделать как можно хуже своему противнику и не обладает разумом. Поэтому и выбор решения в такой ситуации имеет свои особенности.
11.3.3 Обгрунтування рішень на основі змішаних стратегій
В економічній практиці у більшості ігор сідлова точка у чистих стратегіях відсутня, що не дозволяє однозначно визначити оптимальні стратегії гравців. В таких випадках використовуються змішані стратегії, у яких випадковим чином чергуються особисті стратегії. Цей метод широко використовується в господарській практиці, що виражається у стратегії диверсифікації. Наприклад, виробники, не знаючи заздалегідь точних даних щодо попиту, прагнуть розширити асортимент продукції; інвестори вкладають кошти у різні цінні папери і т. д. Отже, гравці намагаються отримати максимальний виграш (мінімальний програш), застосовуючи не одну, а кілька стратегій. Точний метод знаходження оптимальної змішаної стратегії зводиться до задачі лінійного програмування, який досить трудомісткий. Існують спеціальні комп᾽ютерні програми, що реалізують цей метод [машина, сороки, дубров, клименко, ивченко]. Однак можна спробувати знайти оптимальне рішення в умовах конфлікту на основі змішаних стратегій. Змішана стратегія гравця – це повний набір застосування його чистих стратегій при багаторазовому повторенні гри в тих самих умовах із заданими ймовірностями. Умови застосування змішаних стратегій:  - гра не має сідлової точки; - гравці використовують випадкове поєднання чистих стратегій із заданими ймовірностями; - гра багаторазово повторюється в подібних умовах; - при кожному з ходів жоден гравець не інформований про вибір стратегії іншим гравцем; - допускається осереднення результатів ігор [машина, сороки, клименко]. При використанні змішаних стратегій використовують наступні основні положення, наведені у [машина, сороки, дубров, клименко, ивченко]. Для гравця А змішана стратегія полягає в застосуванні чистих стратегій А1, А2, …Аm з відповідними ймовірностями р1, р2, …рm позначається матрицею
за умови, що
Для гравця В
за умови, що
В окремому випадку, коли
Чисті стратегії гравця є єдино можливими неспільними подіями [сороки, клименкоУчебник]. У матричній грі при заданих векторах
де
Шляхом застосування своїх мішаних стратегій гравець А прагне максимально збільшити свій середній виграш, а гравець В – мінімізувати виграш гравця А. Гравець А прагне досягти виконання умови:
Гравець В домагається виконання протилежної умови:
Вектори, що відповідають оптимальним мішаним стратегіям гравців А і В, позначимо як
Ціна гри Розв᾽язком матричної гри є оптимальна змішана стратегія гравця А ( Змішані стратегії будуть оптимальними (
Основна теорема теорії ігор. Для матричної гри з будь-якою матрицею А величини При виборі оптимальних стратегій гравцю А завжди буде гарантований середній виграш, не менший, ніж ціна гри, за будь-якої фіксованої стратегії гравця В (а для гравця В - навпаки). Активними стратегіями гравців А і В називають стратегії, що входять до складу оптимальних змішаних стратегій відповідних гравців з ймовірностями, відмінними від нуля. Отже, до складу оптимальних змішаних стратегій можуть входити не всі апріорі задані їх стратегії. Розглянемо окремий випадок розв᾽язання задач на основі змішаних стратегій. Найпростіша гра може бути описана матрицею 2
Отже, є платіжна матриця:
При цьому
звідки одержуємо оптимальні значення
Знаючи
Обчисливши
Задачу розв᾽язано, оскільки знайдено вектори Це завдання можна розв᾽язати графічним методом, використовуючи наступний алгоритм: - по осі абсцис відкладається відрізок одиничної довжини; - по осі ординат відклажаються виграші при стратегії А1; - на лінії, паралельній осі ординат, у точці 1 відкладаються виграші при стратегії А2; - кінці відрізків позначаються для - визначається ордината точки перетину проведених прямих ліній, яка позначається с. Висота перпендикуляру, опущеного з цієї точки на ось абсцис, дорівнює Графічне зображення цього алгоритму наведено на рисунку 11.1.
Рисунок 11.1 – Графічний метод знаходження оптимальної змішаної стратегії
Даний метод має досить широку сферу використання, що огрунтується на загальній властивості ігор
Контрольні питання
1 Поняття конфліктної ситуації. Причини виникнення конфліктних ситуацій. 2 Особливості розв᾽язання завдань в умовах невизначеності та конфлікту. 3 Система понять теорії ігор. 4 Сутність мажорування стратегій гравців. 5 Порядок обгрунтування рішень на основі чистих стратегій 6 Способи вибору рішень на основі змішаних стратегій.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 285. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,
 ,
, , де
, де  – ймовірність застосування чистої стратегії Вj.
– ймовірність застосування чистої стратегії Вj. , для гравця А маємо чисту стратегію:
, для гравця А маємо чисту стратегію:
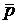 і
і  можна визначити середній виграш гравця А:
можна визначити середній виграш гравця А:
 і
і  – компоненти цих векторів.
– компоненти цих векторів.

 і
і  . Для цих векторів виконується рівність:
. Для цих векторів виконується рівність:
 – середній виграш гравця А при використанні обома гравцями змішаних стратегій.
– середній виграш гравця А при використанні обома гравцями змішаних стратегій.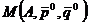 , тобто
, тобто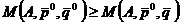 .
. .
. 2. За відсутності сідлової точки можна отримати дві оптимальні змішані стратегії, які записуються так:
2. За відсутності сідлової точки можна отримати дві оптимальні змішані стратегії, які записуються так: ;
;  .
. .
.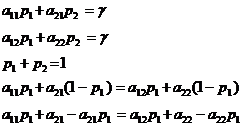
 та
та 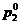 .
.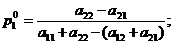


 та
та  :
:
 і ціна гри
і ціна гри  ,
, 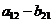 ;
; 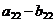 ;
;  та проводяться прямі лінії
та проводяться прямі лінії  та
та  ;
; (
(  ).
). , яка полягає в тому, що у будь-якій грі
, яка полягає в тому, що у будь-якій грі 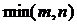 . З цієї властивості випливає, що у будь-якій грі
. З цієї властивості випливає, що у будь-якій грі 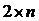 та
та  кожна оптимальна стратегія
кожна оптимальна стратегія  та
та  містить не більш двох активних стратегій. Отже, будь-яка гра
містить не більш двох активних стратегій. Отже, будь-яка гра  і
і  , то для визначення оптимальних змішаних стратегій використовується лінійне програмування. Опис цього розв᾽язання докладно описаний у [івченко, с153].
, то для визначення оптимальних змішаних стратегій використовується лінійне програмування. Опис цього розв᾽язання докладно описаний у [івченко, с153].