
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Игры двух лиц с нулевой суммойИгра двух лиц с нулевой суммой в матричной форме занимает центральное место в современной теории игр, так как теория таких игр разработана практически до конца. Итак, пусть имеется два игрока. В распоряжении первого игрока имеется всего n возможных ходов i=1,2,3,...,n; в распоряжении второго игрока имеется m возможных ходов j=1,2,3,...,n. Эти возможные ходы называются чистыми стратегиямиигроков. Оба игрока делают одновременно по одному ходу, после чего партия считается законченной. Если первый игрок делает ход i, а второй - ход j, то первый игрок получает выигрыш, равный Эти данные можно записать в виде матрицы
в которой строки соответствуют ходу первого игрока, а столбцы - ходу второго игрока. Эта матрица носит название платёжной матрицыигры. Как же должны действовать игроки в такой ситуации? Какие ходы они должны делать?
Игры с седловой точкой Рассмотрим с этих позиций игру со следующей платёжной матрицей
Попробуем порассуждать с точки зрения первого игрока. Если он сделает ход i=1, то наихудшей для него будет ситуация, когда второй игрок сделает ход j=3, так как в этом случае он получит 0. Если первый игрок сделает ход i=2, то в наихудшем случае (при ходе второго игрока j=1) он также получит 0. Аналогично, при i=3 он в наихудшем случае получит 4 (при j=2), при i=4 - 2 (при j=3 ) и, наконец, при i=5 он в наихудшем случае получит 0 (при j=3). Стремясь сделать свой гарантированный выигрыш как можно больше, первый игрок должен выбрать ход i=3, так как в этом случае он гарантирует себе выигрыш, равный 4 (правда, и его максимальный выигрыш невелик - всего 5).  А теперь попробуем посмотреть на эту же матрицу с точки зрения второго игрока. Для него это - матрица его проигрыша. Если он выберет ход j=1, то его максимальный проигрыш будет равен 18 (если первый игрок сделает ход i=1). Аналогично, при j=2 его максимальный проигрыш будет равен 4, при j=3- 8, и, наконец, при j=4 его максимальный проигрыш будет равен 25. Стремясь сделать свой максимальный проигрыш как можно меньше, второй игрок должен выбрать ход j=2, так как в этом случае его максимальный проигрыш, равный 4, самый маленький. Итак, мы пришли к выводу, что первый игрок должен ходить i=3, а второй j=2. Допустим теперь, что второй игрок, как говорят, “открывает карты” и заявляет первому игроку: “Я буду делать ход j=2”. Есть ли первому игроку необходимость менять свой ход? Нет, так как в этом случае его наилучший ход всё равно i=3. Аналогично, если первый игрок заявит второму, что он будет ходить i=3, то второму игроку также нет смысла менять свой ход, так как наилучшим ответом будет всё равно j=2. Пара i=3, j=2 является, как говорят, уравновешенной парой, так как “открытие карт” игроками не даёт поводов противнику менять свою стратегию. Как говорят, пара i=3, j=2 есть решение игры,а величинавыигрыша при этом первого игрока (и одновременно величина проигрыша второго) - 4 - это цена игры. Оформим всё это математически. Итак, пусть первый игрок выбирает ход i. В наихудшей для него ситуации он выиграет
Стремясь сделать свой минимальный выигрыш максимальным, он выбирает свой ход из условия
Такая стратегия называется максиминной. Аналогично, второй игрок, выбирая ход j, в наихудшей для себя ситуации проигрывает
Стремясь сделать свой максимальный проигрыш минимальным, он должен выбирать свой ход из условия
Такая стратегия называется минимаксной. у матрицы может быть несколько седловых точек
Смешанные стратегии Седловая точка в матричных играх всё-таки скорее исключение, чем правило. А что же может гарантировать себе игрок, если седловой точки нет? Давайте снова рассмотрим игру с платёжной матрицей
Здесь Представим себя в позиции первого игрока. Он имеет гарантированный выигрыш (скорее, проигрыш), равный (-1). Как он может его повысить? Конечно, если игра повторяется много раз, то он может изучить своего партнёра, придумывать всякие схемы игры и т.д. и т.п., но вряд ли это даст какие-то гарантии, если число партий невелико. Тут никакие схемы не помогут. В такой ситуации единственный выход - выбирать свой ход случайным образом. Например, взять и подбросить монету. Упадёт она кверху орлом - делать ход i=1, выпадет решка - делать ход i=2. Что же это даст? Выигрыш станет случайной величиной и оценивать его надо по математическому ожиданию. Пусть второй игрок делает ход j=1. Тогда математическое ожидание выигрыша первого игрока будет
Если второй игрок делает ход j=2, то математическое ожидание выигрыша первого игрока равно
Таким образом, выбирая свой ход случайно, первый игрок гарантирует себе (правда, в среднем, а не в каждой партии), выигрыш, равный нулю. А это всё-таки лучше, чем гарантированный выигрыш, равный (-1) . Аналогично, второй игрок, бросая монету и выбирая ход в соответствии с её “указанием”, гарантирует себе в среднем проигрыш, равный 0. Это тоже лучше, чем проигрыш, равный 1. Таким образом, оказывается, что случайный выбор хода повышает наши шансы на успех, хотя бы в среднем. И это является одной из основных идей теории игр - выбиратьсвой ход случайно. Подобный случайный выбор хода получил название смешанной стратегии. Конечно, с обычных житейских позиций, случайный выбор хода не всегда приемлем. Вообразите себе военачальника, который выиграл сражение. Он даёт интервью по TV и на вопрос о том, как же он принял правильное решение, говорит: “Ну, я бросил монету, она упала орлом кверху, и поэтому я … ”. Как посмотрит на него телезритель? А если он проиграл битву, то как отнесётся к такому ответу его начальство? И тем не менее, случайный выбор хода - смешанная стратегия - имеет право на существование, даже в реальной жизни. Когда не знаешь, как действовать - выбирай свой ход случайным образом! Иногда помогает. По крайней мере, никто не разгадает стратегии твоего поведения и не предугадает твоего хода.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 282. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
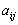 .Очевидно, что выигрыш второго игрока равен
.Очевидно, что выигрыш второго игрока равен  .
. ,
,

 .
.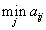 .
. .
. .
.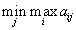 .
. .
. ,
,  и между
и между  и
и  образуется “дыра”
образуется “дыра” 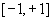 Как можно её заполнить и чем?
Как можно её заполнить и чем? .
. .
.