
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Игры двух лиц с ненулевой суммойРассмотрим теперь основные идеи, касающиеся игр двух лиц с ненулевой суммой. В этом случае игра задаётся двумя матрицами, которые обычно объединяют в одну и пишут в виде
Здесь В такой ситуации появляется принципиально новый момент, которого не было раньше - возможность сговора, совместных действий игроков. Когда И эта возможность сговора не упрощает, а сильно усложняет ситуацию! Потому, что до чего и как договорятся игроки в очень сильной степени зависит от двух вещей: от самой возможности вести переговоры и от психологических особенностей игроков. А психология - очень сложная вещь и математика до неё еще не добралась. Игры двух лиц с ненулевой суммой принято разбивать на два класса - некооперативные и кооперативные. В некооперативных играх игроки не имеют возможности общаться друг с другом. Как же они могут договориться между собой? Это возможно, если игра повторяется - тогда возможность такого сговора появляется в ходе повторения игры, ведь можно наказывать партнёра, выбирая заведомо плохой для него ход. Но вот что из этого получится - теория игр пока не даёт ни ответа, ни совета. В кооперативных играх игроки имеют возможность договариваться в любое удобное для них время и никаких косвенных приёмов для договорённостей им применять не надо.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 294. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
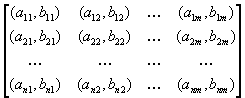
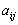 - выигрыш первого игрока и
- выигрыш первого игрока и  - выигрыш второго, если первый игрок делает ход i, а второй - j. Однако в данном случае
- выигрыш второго, если первый игрок делает ход i, а второй - j. Однако в данном случае 

 , то интересы обоих игроков прямо противоположны и возможность сговораисключена в силу противоположности интересов. Если
, то интересы обоих игроков прямо противоположны и возможность сговораисключена в силу противоположности интересов. Если 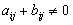 , то интересы игроков могут хотя бы частично совпадать, что и определяет возможность хотя бы частичного сотрудничества между ними.
, то интересы игроков могут хотя бы частично совпадать, что и определяет возможность хотя бы частичного сотрудничества между ними.