
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формула Бернулли. Локальная и интегральная теоремы Муавра-ЛапласаРассмотрим конечную последовательность п независимых испытаний, в результате каждого из которых может произойти событие А или ему противоположное Рn(m) – вероятность того, что событие А произойдёт ровно m раз в серии из n испытаний; Рn(m ≥ k) = Рn(k) + Рn(k + 1) +…+ Рn(n) – вероятность того, что событие A произойдёт не менее k раз в серии из n испытаний; Рn(m ≤ k) = Рn(0) + Рn(1) +…+ Рn(k) – вероятность того, что событие A произойдёт не более k раз в серии из n испытаний; Рn(m ≥ 1) = 1 – Рn(0) – вероятность того, что событие A произойдёт хотя бы один раз в серии из n испытаний. При нахождении нужной вероятности необходимо учитывать заданные значения n и p. При выборе формулы для Рn(m) надо руководствоваться следующими правилами: 1) если задано число испытаний n и оно не больше 10, то надо пользоваться формулой Бернулли Рn(m) = 2) если вероятность р наступления события А мала, а n велико и λ = np < 10, то для Рn(m) надо воспользоваться формулой Пуассона: Рn(m) ≈ 3) если n велико и np > 10, то надо воспользоваться локальной теоремой Муавра-Лапласа. По этой теореме Рn(m) ≈ Имеются таблицы значений функции φ(x), соответствующие положительным значениям аргумента х. Так как функция φ(x) чётная, то φ(– x) = φ(x). И для x > 4 φ(x) ≈ 0.  Если требуется найти вероятность того, что в серии из n независимых испытаний число наступлений события A будет не менее k1 и не более k2 раз, то есть Рn(k1; k2) = Рn(k1 ≤ m ≤ k2), то надо воспользоваться интегральной теоремой Муавра-Лапласа. По этой теореме Рn(k1; k2) ≈ Φ(x2) – Φ(x1), где Φ(x) = Функция Φ(x) называется функцией Лапласа. Она нечётная: Φ(– x) = – Φ(x). Имеются таблицы значений этой функции для соответствующих положительных значений аргумента х. И для х > 5 Ф(х) ≈ 0,5. Рассмотрим примеры применения этих формул.
Пример 4.1.Хлопок определённого сорта имеет 60% коротких волокон. Определите вероятность того, что из 6 случайно взятых волокон будет: а) хотя бы одно короткое волокно; б) ровно 3 коротких волокна; в) не более 3 коротких волокон. Решение. Так как n = 6 < 10, то надо воспользоваться формулой Бернулли. По условию короткие волокна составляют 60%. Значит, вероятность того, что случайным образом взятое волокно будет коротким, равна p = 0,6, следовательно, q = 1 – 0,6 = 0,4. а) Вероятность того, что хотя бы одно из 6 случайно взятых волокон будет коротким, вычисляется по формуле Р6(m ≥ 1) = 1 – Р6(0) = 1 – q6 = 1 – 0,46 = 1 – 0,004096 = 0995904 ≈ 0,996. б) Вероятность того, что среди 6 случайно взятых волокон будет ровно 3 коротких, равна Р6(3) = в) Вероятность того, что среди 6 случайно взятых волокон будет не более 3 коротких волокон, равна Р6(m ≤ 3) = Р6(0) + Р6(1) + Р6(2)+ Р6(3) = 0,46 + + Ответ: а) 0,996; б) 0,28; в) 0,46.
Пример 4.2. Коммерческая фирма рассылает по почте своим клиентам n = 500 писем с проспектами новой продукции. Вероятность того, что при пересылке письмо потеряется, равна р = 0,001. Найти вероятность того, что при пересылке по почте потеряется: а) хотя бы одно письмо с проспектами; б) ровно 3 письма с проспектами; в) не более 3 писем с проспектами. Решение. Количество посланных по почте писем n = 500 велико, а вероятность того, что при пересылке по почте письмо потеряется p = 0,001 мала и λ = np = 0,5 < 10. Следовательно, надо воспользоваться формулой Пуассона: Рn(m) ≈ а) Найдём вероятность того, что при пересылке потеряется хотя бы одно письмо. Р500(m ≥ 1) = 1 – Р500(0) = 1 – (по определению 0! = 1). б) Найдём вероятность того, что при пересылке по почте потеряется ровно 3 письма: Р500(3) ≈ в) Найдём вероятность того, что при пересылке по почте потеряется не более 3 писем: Р500(m ≤ 3) = Р500(0) + Р500(1) + Р500(2)+ Р500(3) = 0,61 + + Ответ: а) 0,40; б) 0,01; в) 1.
Пример 4.3. Пусть вероятность того, что покупателю необходимо купить обувь 27 размера, равна 0,2. Найти вероятность того, что из 400 покупателей, зашедших в магазин, потребуют обувь 27 размера: а) хотя бы один покупатель; б) ровно 90 покупателей; в) не более 90 покупателей. Решение. Так как п = 400 велико, р = 0,2 и λ = np = 80 > 10, то для нахождения требуемых вероятностей необходимо воспользоваться локальной и интегральной теоремами Муавра-Лапласа. По условию задачи
а) Найдём вероятность того, что из 400 покупателей, зашедших в магазин, хотя бы одному потребуется обувь 27 размера: Р400(m ≥ 1) = 1 – Р400(0) = 1 – = 1 – б) Найдём вероятность того, что из 400 покупателей, зашедших в магазин, ровно для 90 покупателей потребуется обувь 27 размера: Р400(90) = = в) Найдём вероятность того, что из 400 покупателей, зашедших в магазин, не более 90 потребуют обувь 27 размера. Здесь k1 = 0, k2 = 90. Тогда P400(0; 90) ≈ Φ(x2) – Φ(x1), где x1 = По таблице значений функции Лапласа находим: Φ(x2) = Φ(1,25) = 0,3944, Φ(x1) = Φ(– 10) = – Φ(10) = – 0,5. Поэтому P400(0; 90) ≈ 0,3944 – (– 0,5) = 0,8944. Ответ: а) 1; б) 0,0228; в) 0,8944.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 258. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
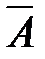 с вероятностями р и q = 1 – p соответственно. При этом будем считать, что вероятность р события А в каждом испытании одна и та же. По условию результат любого испытания не зависит от его порядкового номера и от того, какие исходы были в предыдущих испытаниях. Такую последовательность испытаний принято называть схемой испытаний Бернулли. Приняты следующие обозначения:
с вероятностями р и q = 1 – p соответственно. При этом будем считать, что вероятность р события А в каждом испытании одна и та же. По условию результат любого испытания не зависит от его порядкового номера и от того, какие исходы были в предыдущих испытаниях. Такую последовательность испытаний принято называть схемой испытаний Бернулли. Приняты следующие обозначения: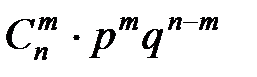 ;
;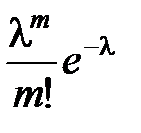 , Рn(m ≤ k) ≈
, Рn(m ≤ k) ≈ 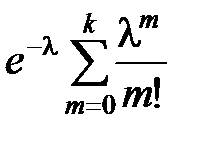 ;
;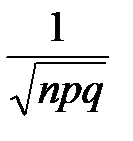 φ(x), где φ(x) =
φ(x), где φ(x) = 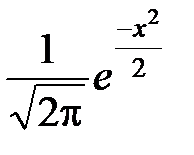 ; x =
; x = 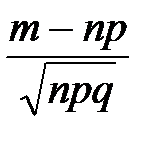 .
.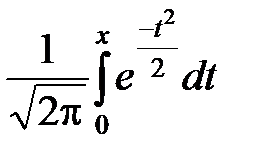 , x1 =
, x1 = 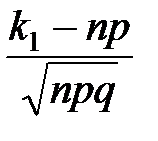 , x2 =
, x2 = 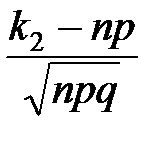 .
.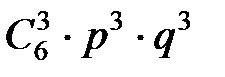 =
= 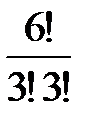 ·0,63·0,63 = 20·0,013824 = 0,27448 ≈ 0,28.
·0,63·0,63 = 20·0,013824 = 0,27448 ≈ 0,28.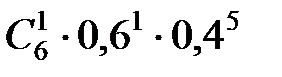 +
+ 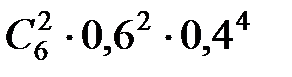 +
+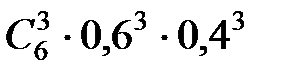 = 0,004096 + 0,036864 + 0,13824 + 0,27648 = 0,45568 ≈ 0,46.
= 0,004096 + 0,036864 + 0,13824 + 0,27648 = 0,45568 ≈ 0,46.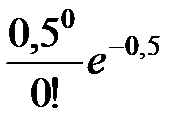 = 1 –
= 1 – 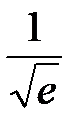 = 1 – 0,60653 ≈ 0,40
= 1 – 0,60653 ≈ 0,40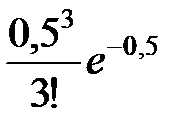 = 0,125·
= 0,125· 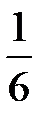 ·
· 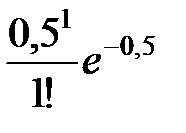 +
+ 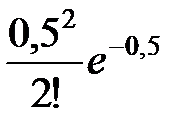 +
+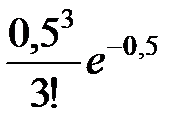 = 0,61 + 0,3 + 0,08 + 0,01 = 1.
= 0,61 + 0,3 + 0,08 + 0,01 = 1.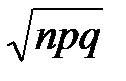 =
= 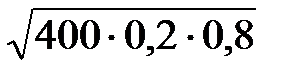 =
= 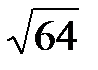 = 8.
= 8.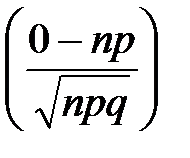 = 1 –
= 1 – 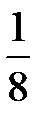 ∙φ
∙φ 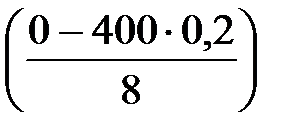 =
=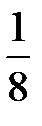 ∙φ(– 10) ≈ 1 – 0 = 1.
∙φ(– 10) ≈ 1 – 0 = 1.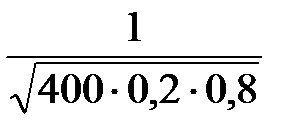 ∙φ
∙φ 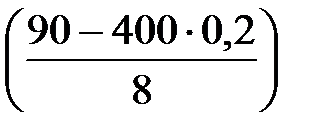 =
= 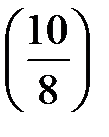 =
= 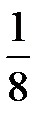 ∙φ(1,25) =
∙φ(1,25) =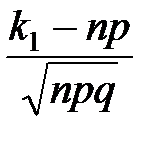 =
= 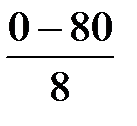 = – 10, x2 =
= – 10, x2 = 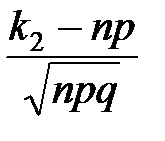 =
= 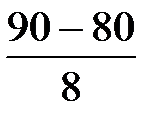 = 1,25.
= 1,25.