
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теоремы сложения и умножения вероятностейСтр 1 из 6Следующая ⇒ ВЫСШАЯ МАТЕМАТИКА
Методические указания и задания к контрольной работе № 3 для студентов-заочников технологических специальностей Могилев 2011 УДК 519.21 517 ББК 22. 1
Рассмотрено и рекомендовано к изданию на заседании кафедры высшей математики Протокол № 13 от 11. 04. 2011 г.
Составители: к. физ.-мат. н., доцент А.М. Гальмак к. физ.-мат. н., доцент В.К. Лапковский ст.пр. И.В. Юрченко
Рецензент к. физ.-мат. н., доцент С.В. Подолян
УДК 519.21 517 ББК 22. 1 © Учреждение образования «Могилевский государственный университет продовольствия», 2011 ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ При оформлении контрольных работ надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для исправлений. 1) Задания контрольной работы студент выбирает по варианту, номер которого совпадает с порядковым номером в списке студенческой группы, который представлен деканатом ЗО. Лектор потока может предложить иную схему выбора номера варианта контрольной работы. 2) Контрольная работа должна быть выполнена в рукописном виде в ученической тетради в клетку, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. Текст должен иметь не более 20 строк на одной стороне листа (ориентировочно – через клетку) с высотой букв и цифр не менее 2,5 мм. Рекомендуемое расстояние между строками в тексте – 5 мм. 3) На обложке тетради должны быть ясно написаны: фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, номер варианта, название дисциплины; здесь же следует указать дату отсылки работы в университет и домашний адрес студента (в соответствии с образцом оформления титульного листа). Выполненные задания должны завершаться списком используемой литературы, проставленной датой ее выполнения и подписью.  4) В работу должны быть включены решения всех задач, соответствующих варианту. Контрольные работы, не содержащие решения всех задач, а также содержащие решения задач не своего варианта, не зачитываются. 5) Решения задач необходимо приводить в последовательности, указанной в контрольной работе. 6) Перед решением каждой задачи надо выписать полностью ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, соответствующими своему варианту. 7) Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя основные действия по ходу решения и делая необходимые чертежи. 8) При получении прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все его рекомендации. Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в кратчайшее время. На повторную проверку обязательно представляется также и ранее прорецензированная работа с рецензией на нее. Вносить исправления в сам текст работы после рецензирования недопустимо. КОНТРОЛЬНАЯ РАБОТА № 3
I СВЕДЕНИЯ ИЗ ТЕОРИИ. ПРИМЕРЫ
Числовые и степенные ряды. Теория вероятностей и математическая статистика Ряды Пусть (ап) = а1, а2, …, ап, … – числовая последовательность. Выражение вида называется числовым рядом, числа а1, а2, …, ап… называются членами ряда, число ап – общим членом ряда. Сумма конечного числа п первых членов ряда Sn = Необходимый признак сходимости: Если ряд (1) сходится, то общий член ряда стремится к нулю при n → ∞: К достаточным признакам сходимости для рядов с положительными членами (ап > 0) относятся следующие признаки: а) Признак сравнения. Пусть даны два ряда с положительными членами • из сходимости ряда • из расходимости ряда б) Признак сравнения в предельной форме. Пусть даны два ряда с положительными членами
Замечание. При применении признаков сравнения в качестве рядов, используемых для сравнения, выбирают, как правило, ряды: 1) геометрический ряд 2) обобщенный гармонический ряд (ряд Дирихле) в) Признак Д′Аламбера. Если для ряда г) Признак Коши. Если для ряда д) Интегральный признак Коши. Если для x ≥ a функция f(x) непрерывна, положительная, не возрастает и, начиная с некоторого номера N, ап = f(n), то ряд Ряд Знакопеременный числовой ряд вида
где ап >0, называется знакочередующимся рядом.
е) Признак Лейбница. Если члены знакочередующегося ряда 1) 2) то этот ряд сходится. Погрешность, возникающая от замены суммы такого сходящегося знакочередующегося ряда суммой его первых n членов, по абсолютной величине не превосходит модуля первого из отброшенных членов: |S – Sn| ≤ ап+1. Ряд вида называется степенным рядом по степеням (х – с), аn – коэффициентами ряда. Число R называется радиусом сходимости степенного ряда (2), если этот ряд сходится абсолютно при всех х, удовлетворяющих условию |x – c| < R и расходится при всех х, удовлетворяющих условию |x – c| > R. При x = c – R и x = c + R ряд может как сходиться, так и расходиться. Интервал (с – R, c + R) называется интервалом сходимости степенного ряда (2), точки с – R и c + R – концами интервала сходимости. Радиус сходимости R может быть найден по формулам: R =
Пример 1.Найти радиус и интервал сходимости степенного ряда и исследовать сходимость ряда на концах интервала сходимости Решение. Для определения радиуса сходимости степенного ряда воспользуемся формулой: R = Так как ап = R = Итак, радиус сходимости ряда R = 5. Определим интервал сходимости данного степенного ряда: |x + 2| < 5 Итак, (– 7; 3) – интервал сходимости степенного ряда. Исследуем сходимость ряда на концах интервала сходимости, то есть в точках х = – 7 и х = 3. Пусть х = – 7. Подставим это значение в исследуемый степенной ряд. Получим знакочередующийся числовой ряд:
Так как Пусть х = 3. Подставив это значение в исследуемый степенной ряд, получим числовой ряд с положительными членами:
Сравним данный ряд с обобщенным гармоническим рядом
Следовательно, оба ряда ведут себя одинаково и исследуемый ряд, как и вспомогательный ряд, расходится. Таким образом, х = 3 не принадлежит области сходимости степенного ряда. Поэтому, областью сходимости исследуемого степенного ряда является полуинтервал [– 7; 3). Ответ: R = 5, [– 7; 3).
Теоремы сложения и умножения вероятностей Рассмотрим n случайных событий A1, A2,…, An. Суммой (объединением) событий A1, A2,…, An называется событие B = A1 + A2 + … + An = Произведением (совмещением) событий A1, A2,…, An называется событие C = A1 · A2 · … · An = События A1, A2,…, An называются попарно несовместными, если в одном и том же опыте никакие два из них не могут произойти вместе. Теорема. Вероятность суммы попарно несовместных событий равна сумме вероятностей этих событий: P(A1 + A2 + … + An) = P(A1) + P(A2) + … + P(An). События А и Случайные события A1, A2,…, An называются независимыми в совокупности, если вероятность появления любого из них не зависит от того, произошли ли какие-либо другие из этих рассматриваемых событий или нет. Теорема. Вероятность произведения случайных событий A1, A2,…, An, независимых в совокупности, равна произведению их вероятностей: P(A1 · A2 · … · An) = P(A1)·P(A2)· … ·P(An).
Пример 2. Вероятности попадания в цель каждым из четырёх независимо друг от друга стреляющих стрелков соответственно равны: 0,9; 0,8; 0,6; 0,7. Стрелки выстрелили в цель одновременно. Найти вероятность того, что произойдёт: а) хотя бы одно попадание; б) не более двух попаданий. Решение. Пусть Ai, i = 1, 2, 3, 4 – события, означающие попадания в цель каждым из четырёх стрелков соответственно, которые являются независимыми в совокупности. Тогда P(A1) = 0,8, P(A2) = 0,9, P(A3) = 0,6, P(A4) = 0,7. Обозначим P( P( а) Событие, состоящее в попадании в цель хотя бы одним стрелком, есть сумма событий: A1 + A2 + A3 + A4. Противоположным для этого события является событие, состоящее в том, что ни один из стрелков не попадёт в цель. Оно может быть представлено в виде произведения независимых в совокупности событий: Р(A1 + A2 + A3 + A4) = 1 – Р( = 1 – P( б) Событие А, состоящее в том, что будет не более двух попаданий, есть сумма несовместных событий, означающих, что попаданий будет или ровно 2, или только 1, или вообще не будет попадания. В символьной записи имеем: А = (A1·A2· + + Применяя теорему о вероятности суммы несовместных событий и теорему о вероятности произведения независимых событий, получим: Р(А) = Р(A1·A2· + Р( + Р( = Р(A1)·Р(A2)·Р( + Р(A1)·Р( + Р( + Р(A1)·Р( + Р( + Р( + 0,2·0,9·0,6·0,3 +0,2·0,9·0,4·0,7 + 0,2·0,1·0,6·0,7 + 0,8·0,1·0,4·0,3 + + 0,2·0,9·0,4·0,3 + 0,2·0,1·0,6·0,3 + 0,2·0,1·0,4·0,7 + 0,2·0,1·0,4·0,3 = 0,2572. Ответ: а) 0,9976; б) 0,2572.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 186. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 =
=  , (1)
, (1)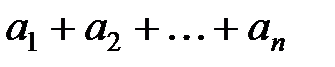 называется n-й частичной суммой ряда. Если существует конечный предел последовательности (Sn) конечных сумм ряда,
называется n-й частичной суммой ряда. Если существует конечный предел последовательности (Sn) конечных сумм ряда,  то ряд (1) называется сходящимся, а число S – суммой данного ряда. В противном случае ряд называется расходящимся.
то ряд (1) называется сходящимся, а число S – суммой данного ряда. В противном случае ряд называется расходящимся. .
. и
и  . Если для членов этих рядов справедливо неравенство 0 < bп ≤ ап,
. Если для членов этих рядов справедливо неравенство 0 < bп ≤ ап,  n ≥ n0
n ≥ n0  N то:
N то: следует расходимость ряда
следует расходимость ряда  = c (c ≠ 0, ∞), то ряды
= c (c ≠ 0, ∞), то ряды  (а ≠ 0), который сходится при |q| < 1 и расходится при |q| ≥ 1;
(а ≠ 0), который сходится при |q| < 1 и расходится при |q| ≥ 1; , который сходится при p > 1 и расходится при p ≤ 1. (В случае p = 1 ряд
, который сходится при p > 1 и расходится при p ≤ 1. (В случае p = 1 ряд  называется гармоническим).
называется гармоническим). = q, то ряд
= q, то ряд  = C, то при С < 1 ряд сходится, а при С > 1 ряд расходится. Если С = 1, то признак Коши не дает ответа на вопрос о сходимости ряда. В этом случае требуется дополнительное исследование.
= C, то при С < 1 ряд сходится, а при С > 1 ряд расходится. Если С = 1, то признак Коши не дает ответа на вопрос о сходимости ряда. В этом случае требуется дополнительное исследование. сходятся или расходятся одновременно.
сходятся или расходятся одновременно. с членами, имеющими разные знаки, называется условно сходящимся, если ряд
с членами, имеющими разные знаки, называется условно сходящимся, если ряд  расходится, и абсолютно сходящимся, если ряд
расходится, и абсолютно сходящимся, если ряд  сходится.
сходится. =
= 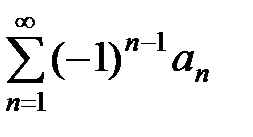 ,
, (ап > 0) удовлетворяют условиям:
(ап > 0) удовлетворяют условиям: ;
; ,
, =
=  , (2)
, (2) или R =
или R =  .
. .
. .
. и ап + 1 =
и ап + 1 =  , то
, то =5
=5 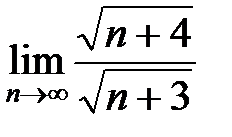 =5
=5  =5
=5  =5.
=5. – 5< x + 2 < 5
– 5< x + 2 < 5  – 7 < x < 3.
– 7 < x < 3. =
= 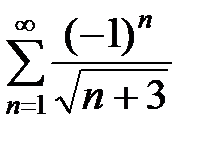 .
. и
и  = 0, то согласно признаку Лейбница данный ряд сходится. Таким образом, х = – 7 принадлежит области сходимости степенного ряда.
= 0, то согласно признаку Лейбница данный ряд сходится. Таким образом, х = – 7 принадлежит области сходимости степенного ряда. =
=  .
. при р =
при р =  < 1, который является расходящимся. Для исследования на сходимость применим предельный признак сравнения. Получим
< 1, который является расходящимся. Для исследования на сходимость применим предельный признак сравнения. Получим = 1 ≠ 0.
= 1 ≠ 0. , состоящее в появлении хотя бы одного из рассматриваемых событий.
, состоящее в появлении хотя бы одного из рассматриваемых событий. , обозначающее появление всех перечисленных событий.
, обозначающее появление всех перечисленных событий.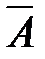 называются противоположными, если это два единственно возможных события в данном испытании. Событие
называются противоположными, если это два единственно возможных события в данном испытании. Событие  состоит в не наступлении события A. Очевидно, события A и
состоит в не наступлении события A. Очевидно, события A и  несовместны, поэтому P(
несовместны, поэтому P(  , i = 1, 2, 3, 4 – события, означающие непопадания в цель каждым из четырёх стрелков.
, i = 1, 2, 3, 4 – события, означающие непопадания в цель каждым из четырёх стрелков.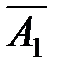 ) = 1 – 0,8 = 0,2; P(
) = 1 – 0,8 = 0,2; P(  ) = 1 – 0,9 = 0,1; P(
) = 1 – 0,9 = 0,1; P(  ) = 1 – 0,6 = 0,4;
) = 1 – 0,6 = 0,4; ) = 1 – 0,7 = 0,3.
) = 1 – 0,7 = 0,3. ·
·  ·
·  ·
·  . По теореме о вероятности произведения независимых в совокупности событий имеем:
. По теореме о вероятности произведения независимых в совокупности событий имеем: ) = 1 – Р(
) = 1 – Р(  ·
·  ·
·  ·
·  ) =
) = ·A3·
·A3· 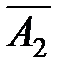 ·
·  ·A4 +
·A4 +  ·A2·A3·
·A2·A3·  ·A2·
·A2·  ·A4 +
·A4 +  ·A3·A4) + (A1·
·A3·A4) + (A1·  ·
·  ·A2·
·A2·  ·
·  ·A3·
·A3·  ·
·  ·
·  )·Р(A3)·Р(
)·Р(A3)·Р(  )·Р(
)·Р(  )·Р(A4) + Р(
)·Р(A4) + Р(  )·Р(A2)·Р(A3)·Р(
)·Р(A2)·Р(A3)·Р(  )·Р(
)·Р( 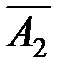 )·Р(A3)·Р(A4) +
)·Р(A3)·Р(A4) +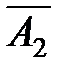 )·Р(
)·Р(  )·Р(A2)·Р(
)·Р(A2)·Р(  )·Р(
)·Р(  )·Р(A3)·Р(
)·Р(A3)·Р(