
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Интегрирование тригонометрических функций. ⇐ ПредыдущаяСтр 7 из 7 Задача 39. Вычислить интеграл Решение. Функция не обладает свойствами чётности или нечётности, то есть, сменив знак синуса или косинуса, мы не получим, что знак минус будет у всей дроби. Поэтому применяем универсальную тригонометрическую подстановку:
Итак, сделаем замену:
Теперь сделаем обратную замену. Ответ. Примеры на другие подстановки. Задача 40. Вычислить интеграл Решение. Здесь нечётная степень синуса, применяем замену Ответ. Замечание. Универсальная подстановка здесь приводит к огромным вычислениям. Попробуем применить её:
Если раскрыть скобки в числителе, и разбить на сумму множества дробей, то в знаменателе каждой из них будет Задача 41. Вычислить интеграл Решение. Сделаем замену
это можно после обратной замены и применения свойств логарифмов, записать так: Ответ. Задача 42. Вычислить интеграл Решение. Здесь тоже суммарная степень чётная, замена
здесь мы воспользовались формулой
После обратной замены получаем ответ: Ответ. Задача 43. Вычислить интеграл Решение. Здесь суммарная степень чётная, то есть, если сменить знак перед sin и cos, то знак сменится 2 раза, и останется «+». Поэтому надо применить замену 
После обратной замены получается: Ответ. Проверка. Задача Д-15. Вычислить интеграл Решение. Функция нечётная относительно косинуса, замена Тогда Однако в этом примере квадратные корни не сокращаются, а наоборот, умножаются, ведь косинус теперь не в числителе, а в знаменателе: Но всё равно, будет чётная степень корня: Итак, Теперь мы можем воспользоваться тем разложением, которое получали для такого случая в теме «рациональные дроби» на прошлой практике, см. задачу 33, где оба корня знаменателя кратные. Курс специально построен так, чтобы использовать некоторые коэффициенты из старых примеров и не искать их здесь повторно. Разложение было такое: После приведения к общему знаменателю и решения системы уравнений, там получалось Итак, =
Сделаем обратную замену. Ответ.
Далее: Взаимосвязь иррациональностей и тригонометрических функций. Примеры с интегралами, содержащими
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 160. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. 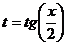 . Напомним, что при этом
. Напомним, что при этом ,
,  ,
, 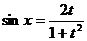 ,
,  .
.  =
=  =
=  =
= =
=  =
=  .
. , что ещё можно привести к виду
, что ещё можно привести к виду  .
. .
. . Тогда
. Тогда 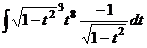 =
=  =
= =
=  =
=  =
=  .
. =
=  .
. , то есть каждое слагаемое надо будет вычислять по рекуррентной формуле в 12 шагов.
, то есть каждое слагаемое надо будет вычислять по рекуррентной формуле в 12 шагов. .
.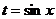 .
. =
=  вот и свелось к рациональной дроби, и дальше для t можем действовать в рамках прошлой темы «рациональные дроби».
вот и свелось к рациональной дроби, и дальше для t можем действовать в рамках прошлой темы «рациональные дроби». =
=  =
= 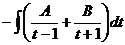 . Приводим к общему знаменателю:
. Приводим к общему знаменателю: =
= 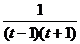 , далее
, далее 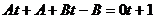 ,
, , отсюда следует
, отсюда следует 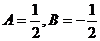 .
. =
= 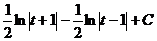
 .
. .
.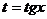 .
. .
. 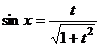 ,
,  .
.  =
=  =
= =
=  =
= 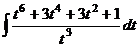
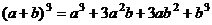 .
. =
=  .
. .
.  .
. =
=  =
=  =
=  =
=  =
=  .
.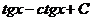 .
. .
. ,
,  ,
,  .
.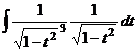 .
. .
. , что равно
, что равно  =
= 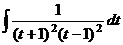 .
. .
.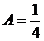 ,
,  ,
,  ,
,  .
.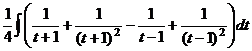 =
= =
= =
= 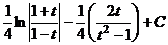 .
. .
. .
. , решаемые с помощью тригонометрических функций.
, решаемые с помощью тригонометрических функций.