
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Рациональные дроби. Случай 3. Если есть комплексные корни.Задача 35 (Э). Вычислить интеграл Решение. Запишем разложение на простейшие дроби: Это равно Тогда
Тогда Во втором слагаемом, можно подвести под знак дифференциала:
Ответ. Задача Д-13. Вычислить интеграл Решение. Применим формулу, при этом n+1 = 2 (n=2 было бы неправильно, ведь в формуле та степень, которую выражаем, это n+1 а та, через которую, это n). При этом n = 1. a = 1. Формула приобретает такой вид: Ответ. Задача Д-14. Вычислить интеграл Решение. Применим формулу суммы кубов Знаменатель дальше разложить невозможно, ведь во второй скобке отрицательный дискриминант. Теперь извлечём дробь и разложим на простейшие.
Тогда
Система уравнений:
на последнем этапе, от 3 строки отняли 2-ю. Получили систему:
Тогда надо рассматривать такую сумму интегралов:
Разбили дробь так, чтобы в одной части подвести под знак дифференциала, а во второй в числителе 1, там можно выделить полный квадрат и свести к арктангенсу. Модуль во втором логарифме не нужен, так как там у выражения отрицательный дискриминант, т.е. нет корней, оно положительно.
Ответ. Интегрирование иррациональностей. Задача 36.Вычислить интеграл Решение. Здесь есть корни порядка 2 и 3. Наименьшее общее кратное, НОК(2,3) = 6. Поэтому замена
Тогда
Сделаем обратную замену и получим: Ответ. Задача 37. Вычислить интеграл  Решение. Здесь также корни порядка 2 и 3, НОК(2,3) = 6. Замена
Во втором интеграле надо разложить на простейшие дроби.
Тогда
Ответ.
Задача 38. Вычислить интеграл Решение. Сначала сделаем замену Но внешний корень ещё не устранили, поэтому сделаем 2-ю замену:
После второй замены, уже получили интеграл от степенных функций!
Сделаем обратную замену:
Ответ. |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 181. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.  .
. .
.  .
. , итого
, итого 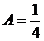 ,
,  ,
,  .
.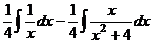 .
. =
=  =
=  .
. с помощью рекуррентной формулы
с помощью рекуррентной формулы 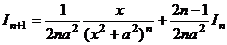 .
. .
. .
.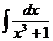 .
. =
=  .
. =
=  . Тогда
. Тогда (приравняли числители этой дроби и той исходной, что была в интеграле).
(приравняли числители этой дроби и той исходной, что была в интеграле). .
.
 , решая её методом Гаусса, получаем:
, решая её методом Гаусса, получаем:



 , здесь
, здесь  ,
,  ,
,  .
. =
=  =
= =
= =
=
 =
= .
. 
 .
.  . При этом,
. При этом,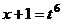 ,
,  ,
,  ,
, ,
, .
.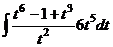 =
=  =
= =
=  .
. .
. .
.  . При этом,
. При этом,  ,
, 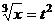 ,
,  .
. =
=  =
= 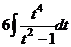 =
= =
=  =
= .
. .
. , откуда получаем
, откуда получаем
 , то есть
, то есть 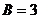 ,
,  .
. =
=  =
=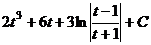 . После обратной замены:
. После обратной замены: .
. .
. 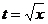 . При этом
. При этом  , значит,
, значит,  . Тогда
. Тогда 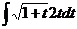 .
. . Тогда
. Тогда  ,
,  ,
,  , соответственно:
, соответственно: =
= 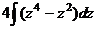 .
. .
. , и после обратной замены:
, и после обратной замены:  .
.