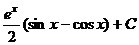Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
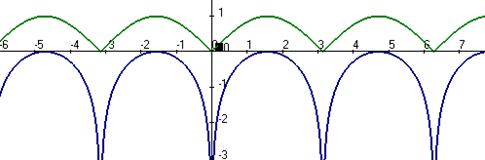
Подведение под знак дифференциала.Задача 10. Вычислить Решение. Замечаем, что присутствует множитель Применяем замену Далее, Ответ. Задача 11.Вычислить интеграл Решение. = Ответ. Задача 12. Вычислить Решение. Ответ. Для сведения, покажем, как выглядит график функции Зелёным цветом изображён график Вертикальные асимптоты
Задача 13. Вычислить интеграл Решение.
Ответ. Д-1.Вычислить интеграл Д-2. Вычислить интеграл Д-3.Вычислить интеграл Д-4. Вычислить интеграл Задача 14. Вычислить Решение. Ответ. Задача 15 (Э). Вычислить Решение. Если сразу подвести под знак дифференциала то, что есть в числителе, то будет
и теперь, после замены Далее, сделаем преобразование, котрое позволит оставить только однотипные корни:
далее уже с помощью обычных действий со степенными функциями:
После обратной замены получаем ответ, при этом также заодно обратно меняем дробные степени на корни. Ответ. Задача 16. Вычислить Решение. =
 Ответ. Задача 17. Вычислить Решение. Несмотря на то, что интеграл похож на
после замены переменной, это можно переписать так: а значит, Ответ. Задача 18 (Э). Вычислить Решение. Для того, чтобы применить формулу, нужно обозначить
Теперь интеграл имеет вид После обратной замены получаем ответ. Ответ. Д-5. Вычислить Решение. Д-6. Вычислить Решение. = Ответ. Д-7.Вычислить Указание. См. задачу 14. Д-8. Вычислить Задача 19. Вычислить Решение. Заметим, что в числителе производная того выражения, которое есть в знаменателе. Тогда Здесь фактически мы применили замену Ответ.
Задача 20. Вычислить Решение. Здесь, в отличие от прошлой задачи, в числителе уже произвольный многочлен, не соответствующий производной от знаменателя. Тем не менее, можно путём арифметических операций получить там дифференциал знаменателя: Домножим и поделим на 2, чтобы исправился коэффициент при
Теперь осталось прибавить и отнять 2, и будет получено
= В первом слагаемом делается ровно то же самое, что в прошлой задаче, а во втором - выделить полный квадрат, и в итоге сводится к арктангенсу:
Ответ.
Задача 21. Вычислить интеграл Решение. В отличие от прошлой задачи, здесь не надо прибавлять и вычитать, так как полный дифференциал знаменателя это Далее, Ответ.
«Интегрирование по частям» 0. Вспомнить формулу Задача 22. Вычислить Решение. Пусть
Тогда Ответ. Задача 23. Вычислить интеграл Решение.
Задача 24 (Э). Вычислить интеграл Решение. Так как степенная функция 2-й степени, то эта задача решается в 2 шага. На первом шаге, обозначаем
Тогда На 2-м шаге, обозначим
В скобке происходит вычисление как бы для нового примера, выполним это вложенное действие:
Итак, ответ:
Задача 25 (Э). Вычислить интеграл Решение. Пусть Построим таблицу:
Тогда
Ответ:
Задача 26 (Э). Вычислить интеграл Производная арктангенса это рациональная дробь. И это мы используем, обозначая её
Тогда: Второе слагаемое далее уже решается подведением под знак dx.
Замечание. Если при переходе от
=
Задача 27 (Э). Вычислить интеграл Решение. Пусть . На первом шаге, обозначаем
На 2-м шаге, в том интеграле, который получился, обозначим аналогичным образом:
Получается Из равенства
Примечание. Интегралы вида Ответ.
Д-9. Вычислить Решение. На первом шаге,
Продолжим преобразования:
После двух действий, мы видим снова интеграл Можно записать так, раскрыв скобки:
Ответ. Д-10. Вычислить Ответ.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 222. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
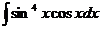 .
.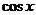 , который является производной от
, который является производной от 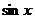 . А остальная часть функции как раз зависит только от
. А остальная часть функции как раз зависит только от 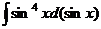
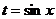 :
: 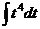 .
. , и после обратной замены
, и после обратной замены 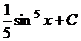 .
.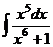 .
.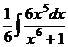 =
= 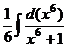 =
= 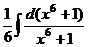 =
= 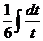 =
=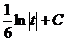 =
= 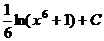 . Учитывая тот факт, что
. Учитывая тот факт, что 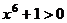 , знак модуля не нужен.
, знак модуля не нужен. .
. 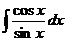 =
= 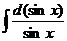 =
= 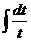 =
= 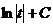 =
= 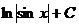 .
. 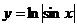 .
.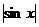 , синим
, синим 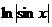 .
. .
.
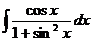 .
. 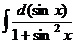 =
= 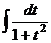 =
= 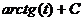 =
=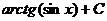 .
. 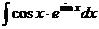 . Ответ.
. Ответ. 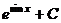 .
.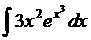 . Ответ.
. Ответ. 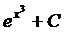 .
.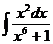 . Ответ.
. Ответ. 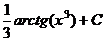 .
.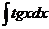 . Ответ.
. Ответ. 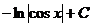 .
.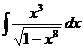 .
.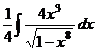 =
= 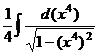 =
= 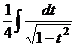 =
=  =
= 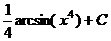 .
.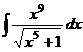 .
.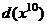 , но тогда в знаменателе получится выражение
, но тогда в знаменателе получится выражение 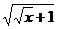 . чтобы не происходило такого усложнения и не появились вложенные квадратные корни, надо подводить не весь числитель, а отделить тот множитель, который нам удобнее, чтобы потом всё выражалось через
. чтобы не происходило такого усложнения и не появились вложенные квадратные корни, надо подводить не весь числитель, а отделить тот множитель, который нам удобнее, чтобы потом всё выражалось через 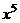 .
.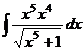 =
= 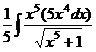 =
= 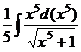
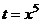 , получится
, получится 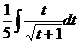 .
.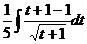 =
= 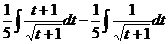 =
=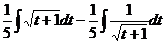 =
= 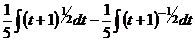
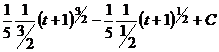 =
= 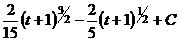 .
.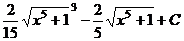 .
.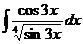 .
.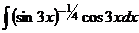 =
=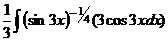 =
= 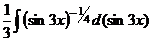 =
= 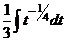 =
= =
= 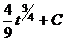 =
= 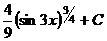 .
.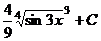 .
.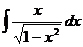 .
.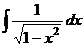 , но, тем не менее, в числителе есть переменная
, но, тем не менее, в числителе есть переменная 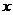 , поэтому это не табличный интеграл, и ответ здесь вовсе не арксинус. Заметим, что в числителе 1-я степень, а под корнем в знаменателе 2-я. Домножим и поделим так, чтобы в числителе оказалось то выражение, которое под корнем в знаменателе.
, поэтому это не табличный интеграл, и ответ здесь вовсе не арксинус. Заметим, что в числителе 1-я степень, а под корнем в знаменателе 2-я. Домножим и поделим так, чтобы в числителе оказалось то выражение, которое под корнем в знаменателе.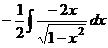 =
= 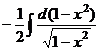
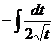
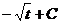 и после обратной замены:
и после обратной замены: 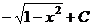 .
.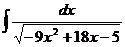 .
.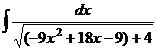 =
= 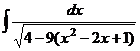 =
= 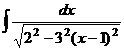 =
= 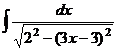 .
.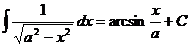
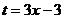 . Но сначала сделаем так, чтобы и в числителе оказался не просто
. Но сначала сделаем так, чтобы и в числителе оказался не просто  а
а 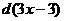 :
: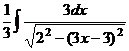 =
= 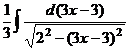 .
.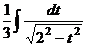 , и равен
, и равен 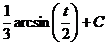 .
.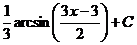 .
.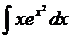 .
.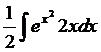 =
= 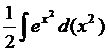 =
= 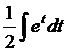 =
= 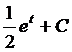 =
= 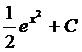 . Ответ.
. Ответ. 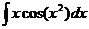 .
.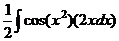 =
= 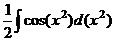 =
=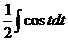 =
=  =
= 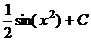 .
. 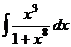 Ответ.
Ответ. 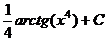 .
.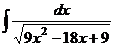 при
при 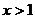 . Ответ.
. Ответ. 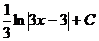 . Указание. См. задачу 18.
. Указание. См. задачу 18.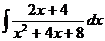 .
. 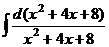 =
= 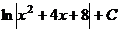 .
.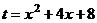 для упрощения выражения. Кстати, выделение полного квадрата в знаменателе это здесь был бы тупиковый путь, ведь в числителе не константа а многочлен, то есть не удалось бы свести к виду
для упрощения выражения. Кстати, выделение полного квадрата в знаменателе это здесь был бы тупиковый путь, ведь в числителе не константа а многочлен, то есть не удалось бы свести к виду 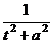 .
.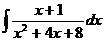 .
. 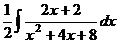
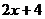 :
: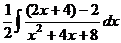 =
=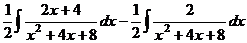 .
.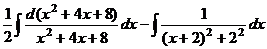 =
=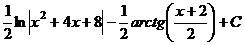 .
.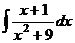 .
.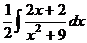 =
= 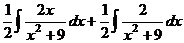
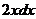 , в знаменателе нет 1-й степени, а его производная поэтому не содержит константу.
, в знаменателе нет 1-й степени, а его производная поэтому не содержит константу.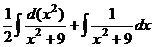 =
= 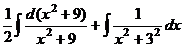 , и в итоге:
, и в итоге: 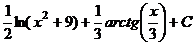 .
.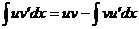 .
.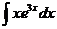 .
.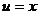 , так надо, чтобы понизилась степень на следующем шаге. Составим таблицу:
, так надо, чтобы понизилась степень на следующем шаге. Составим таблицу: 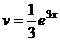
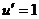
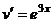
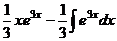 =
= 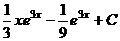 .
.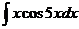 .
.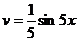
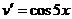
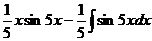 =
= 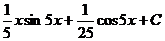 .
. .
. 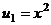 ,
, 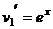 .
.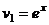
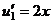
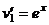
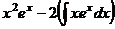 .
.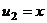 ,
, 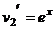 .
.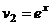
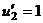
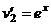
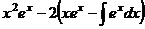 =
= 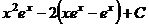 .
.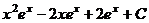 .
.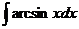
 , второго множителя нет, но мы формально можем считать, что он есть, только равен 1. Итак,
, второго множителя нет, но мы формально можем считать, что он есть, только равен 1. Итак, 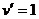 .
.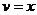
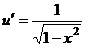
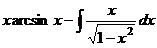 =
=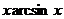
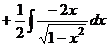 =
= 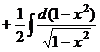 =
=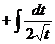 =
= 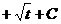 .
. 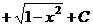 .
.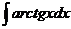
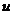 при интегрировании по частям:
при интегрировании по частям: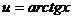
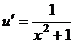
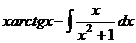 .
.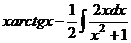 =
=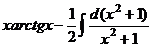 =
= 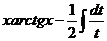 =
=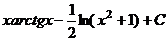 . Знак модуля даже не нужен, т.к.
. Знак модуля даже не нужен, т.к. 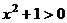 .
.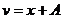 , то это не повлияет на ответ, потому что дополнительное слагаемое всё равно сокращается в итоге:
, то это не повлияет на ответ, потому что дополнительное слагаемое всё равно сокращается в итоге: 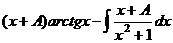 =
= 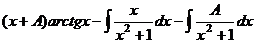
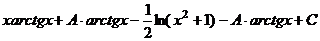 .
.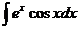
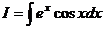 .
. 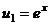 ,
, 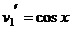 .
.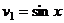
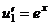
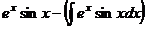 .
.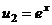 ,
,  .
.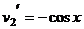
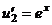
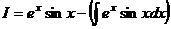 =
= 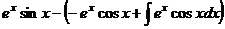 =
= 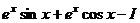 .
.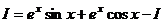 можно выразить
можно выразить 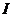 :
: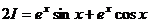 ,
, 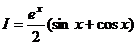 .
.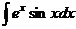 называются «циклические интегралы», потому что они решаются таким способом: через 2 цикла вычисления получается сведение к исходному интегралу.
называются «циклические интегралы», потому что они решаются таким способом: через 2 цикла вычисления получается сведение к исходному интегралу.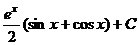 .
.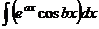 . Указание. См. задачу 27.
. Указание. См. задачу 27.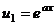
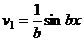
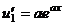
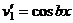
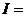
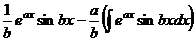 . Теперь в скобках аналогичное выражение, применим к нему такие же преобразования.
. Теперь в скобках аналогичное выражение, применим к нему такие же преобразования. 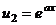
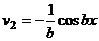
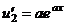
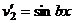
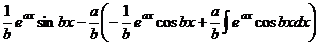 .
.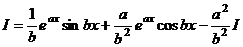 . А теперь можно просто выразить это
. А теперь можно просто выразить это 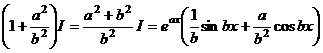
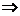
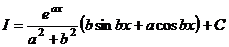 .
.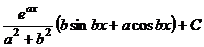 .
.