
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Рациональные дроби. Случай 2. Если есть кратные корни.Задача 32. Вычислить интеграл Решение. Как видим, здесь корень 1 имеет кратность 2. Разложение на простейшие дроби нельзя проводить так, как будто бы здесь три независимых множителя Приведём к общему знаменателю:
Числитель этой дроби равен числителю исходной, той, которая была в интеграле:
Система приведена к виду: Тогда В 1 и 3 слагаемых - как раньше, а вот во 2-м логарифм в ответе не получится, ведь тут уже 2-я а не 1-я степень в знаменателе. Полезно вспомнить, что То есть, интеграл от -2 степени будет содержать -1 степень, и меняется знак. Ответ.
Задача 33 (Э). Вычислить интеграл Решение. Сначала запишем знаменатель подробнее, с учётом корней: Это тот случай, когда оба корня кратные, кратности 2. Разложение на простейшие дроби будет иметь такой вид:
После приведения к общему знаменателю, в числителе будет такое выражение:
здесь при А и С можно один множитель отделить от 2-й степени, с тем чтобы образовать выражение типа
= перегруппируем слагаемые, чтобы вынести каждую степень отдельно: Этот многочлен равен
Построим расширенную матрицу и применим метод Гаусса: Сначала обнулим всё ниже чем 
Ниже
Тогда в интеграле функция распадается на сумму 4 слагаемых:
из всех вынесли общий коэффициент
Ответ.
Задача 34 (Э). Вычислить интеграл Решение. Здесь корень 0 имеет кратность 2, остальные корни простые.
После приведения к общему знаменателю, числитель будет такой:
После приведения подобных:
то матрицу 4 порядка для метода Гаусса строить не надо, а останется только маленькая система на C,D.
Ответ. Задача Д-11. Вычислить Решение. В данном примере D>0, в отличие от предыдущих. Нужно сначала разбить дробь на сумму простейших:
и после этого, будет сумма двух таких интегралов, каждый из которых сводится к логарифму. Чтобы найти А и В, приведём к общему знаменателю:
Теперь приравняем числители, ведь дроби равны, знаменатели одинаковы, значит и числители тоже:
Отсюда получается система уравнений, из которой можно найти неопределённые коэффициенты А и В:
Решая эту систему, получаем
Ответ. Задача Д-12. Вычислить интеграл Решение. Сначала разложим знаменатель на множители:
Ответ. |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 158. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.  ,
,  , т.е.
, т.е.  , иначе получится противоречие, ведь общий знаменатель будет содержать всего лишь 1-ю степень
, иначе получится противоречие, ведь общий знаменатель будет содержать всего лишь 1-ю степень 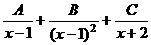 .
.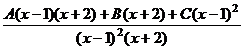 .
. .
. , система:
, система: . Построим расширенную матрицу и решим систему уравнений:
. Построим расширенную матрицу и решим систему уравнений:


 .
.
 ,
,  ,
, 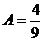 . И теперь интеграл распадается на сумму трёх интегралов:
. И теперь интеграл распадается на сумму трёх интегралов:  .
. .
. .
. .
. =
=  .
. .
. =
= тогда привести подобные легче.
тогда привести подобные легче. =
=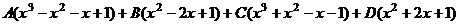 .
.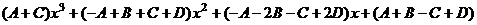 .
. , таким образом, получается система уравнений:
, таким образом, получается система уравнений:
 , затем ниже
, затем ниже  .
.


 можно уже и не обнулять, ведь идея метода Гаусса состоит в том, чтобы количество неизвестных снижалось, вплоть до одной в последнем уравнении, а здесь уже так и есть, в последнем уравнении всего один элемент. Сначала выразим
можно уже и не обнулять, ведь идея метода Гаусса состоит в том, чтобы количество неизвестных снижалось, вплоть до одной в последнем уравнении, а здесь уже так и есть, в последнем уравнении всего один элемент. Сначала выразим 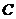 , затем через неё
, затем через неё  и так далее. Система может быть представлена в виде:
и так далее. Система может быть представлена в виде:
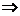
 ,
,  ,
,  ,
, 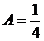 .
.
 , и перед третьим слагаемым поставили знак минус. Получается:
, и перед третьим слагаемым поставили знак минус. Получается: =
= =
=  .
. .
. =
=  .
. =
=  .
. .
.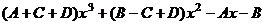 , это надо приравнять к
, это надо приравнять к Поскольку A,B определяются сразу же,
Поскольку A,B определяются сразу же,  ,
,  ,
, тогда
тогда  ,
,  .
.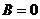 , иначе возникло бы противоречие при приведении к общему знаменателю.
, иначе возникло бы противоречие при приведении к общему знаменателю. =
=  .
. .
.
 =
=  .
.

 .
.
 ,
, 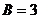 . Тогда интеграл распадается на простейшие:
. Тогда интеграл распадается на простейшие: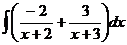 =
=  .
. .
. .
. .
. =
=  =
= 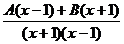 .
.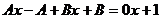 , тогда
, тогда , отсюда
, отсюда  ,
,  .
. =
=  =
=  .
.