
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Кинематика ременных передач
Окружные скорости, м/с, на шкивах (см. рис.1):
где d1 и d2 – диаметры ведущего и ведомого шкивов, мм; n1 и n2 – частоты вращения шкивов, мин-1. Окружная скорость на ведомом шкиве v2 меньще скорости на ведущем v1 вследствие скольжения:
где ε =0,01…0,02 – коэффициент скольжения Передаточное отношение
Геометрические параметры передачи Основными геометрическими параметрами открытой ременной передачи (рис.2) являются: диаметры шкивов d1 и d2, межосевое расстояние Диаметры шкивов определяются в зависимости от типа привода, передаваеиой мощности и передаточного отношения. Диаметры шкивов плоскоременных и клиноременных передач стандартизованы. Межосевое расстояние При геометрическом расчете известными являются Рис. 2 Геометрические параметры ременной передачи Угол между ветвями ремня находят из треугольника О1СО2:
Учитывая, что
Угол обхвата ремнем малого шкива в градусах:
Длина ремня определяется как сумма прямолинейных участков и дуг обхвата:
При заданной длине ремня межосевое расстояние
Нагрузка на валы и опоры Силы натяжения ветвей ремня (за исключением  Рис. 5 Силы, действующие на вал передачи Равнодействующая нагрузка на вал
Обычно Силы и напряжения в ремне Окружная сила на шкивах, Н,
где Из условия равновесия шкива при передаче вращающего момента
где
где Из равенств (9) и (10) следует
Сила начального натяжения ремня Уравнения (11) не вскрывают способности передачи передавать нагрузку Соотношение сил натяжения ведущей и ведомой ветвей ремня определяют по уравнению Эйлера
где Из формулы (12) видно, что нагрузочная способность ременной передачи возрастает с увеличением Нагрузочная способность ременной передачи понижается в результате действия центробежной силы
где Предварительное напряжение
Полезное напряжение
Напряжения
Напряжения
Кроме вышеуказанных напряжений в ремне при огибании шкивов возникают напряжения изгиба
где Суммарное максимальное напряжение в ведущей ветви в месте набегания ремня на малый шкив
Эпюра распределения напряжений по длине ремня показана на рис.3.
Рис.3. Эпюры напряжений в ремне |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 510. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  , (1)
, (1)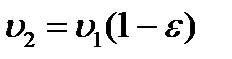 , (2)
, (2) (3)
(3) , угол
, угол  между ветвями ремня, угол обхвата
между ветвями ремня, угол обхвата  ремнем малого шкива и длина ремня
ремнем малого шкива и длина ремня  .
. и
и 

 практически не превышает 150 то
практически не превышает 150 то (4)
(4) ;
;  (5)
(5)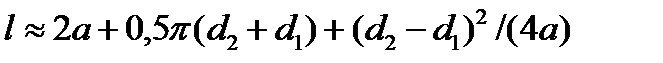 (6)
(6) (7)
(7) ) передаются на валы и опоры (рис.5).
) передаются на валы и опоры (рис.5).
 (21)
(21) что относится к недостаткам ременной передачи.
что относится к недостаткам ременной передачи. (8)
(8) -вращающий момент, Нм, на ведущем шкиве диаметром
-вращающий момент, Нм, на ведущем шкиве диаметром  .
. , (9)
, (9) и
и  - силы натяжения ведущей и ведомой ветвей ремня под нагрузкой. Так как геометрическая длина ремня от нагрузки не зависит, то можно записать равенство суммарных натяжений ветвей в нагруженной и ненагруженной передаче:
- силы натяжения ведущей и ведомой ветвей ремня под нагрузкой. Так как геометрическая длина ремня от нагрузки не зависит, то можно записать равенство суммарных натяжений ветвей в нагруженной и ненагруженной передаче: (10)
(10) - сила начального натяжения ремня.
- сила начального натяжения ремня.
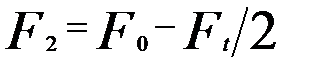 . (11)
. (11) , т.е. тяговой способности передачи.
, т.е. тяговой способности передачи. (12
(12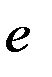 - основание натурального логарифма;
- основание натурального логарифма;  - коэффициент трения;
- коэффициент трения;  , (13)
, (13) - плотность материала ремня;
- плотность материала ремня;  - площадь поперечного сечения ремня.
- площадь поперечного сечения ремня.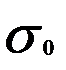 в ремне равно
в ремне равно . (14)
. (14)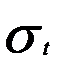 в ремне от окружной силы
в ремне от окружной силы  . (15)
. (15)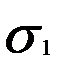 и
и  в ветвях ремня от рабочей нагрузки равны
в ветвях ремня от рабочей нагрузки равны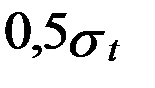 ;
;  в ремне от действия центробежной силы
в ремне от действия центробежной силы 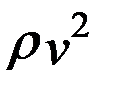
 (17)
(17)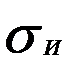 ,которые определяются по формуле
,которые определяются по формуле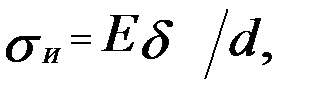 (18)
(18) - модуль упругости;
- модуль упругости; 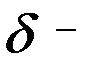 толщина ремня.
толщина ремня. (19)
(19)