Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Геометрические и кинематические параметрыСтр 1 из 10Следующая ⇒ Планетарные передачи Планетарными называют передачи, содержащие зубчатые колеса с перемещающимися осями (рис 1,а). передача состоит из центрального колеса Ведущим в планетарной передаче может быть либо центральное колесо, либо водило. При заданной угловой скорости ведущего звена угловые скорости остальных звеньев получают вполне определенные значения, поэтому планетарная передача имеет постоянное передаточное отношение. Планетарные передачи могут быть одно — и многоступенчатыми. Достоинства планетарных передач:
Недостатки планетарных передач:
Планетарные зубчатые передачи широко распространены в машиностроении и приборостроении. Кинематика планетарных передач. Передаточное отношение обозначают буквой с индексами, например  При исследовании кинематики планетарных передач используют метод остановки водила – метод Виллиса. Всей планетарной передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. Получим обращенный механизм (рис.1,в), представляющий собой простую передачу, в которой движение передается от Для обращенного механизма
(6,1)
В планетарных передачах существенное значение имеет знак передаточного отношения. При Для реального механизма у которого колесо
или
(6.2)
Частоту вращения сателлита определим из равенства
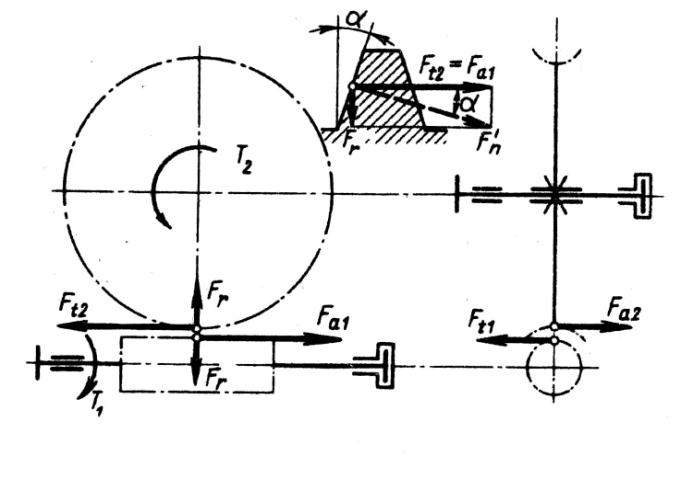
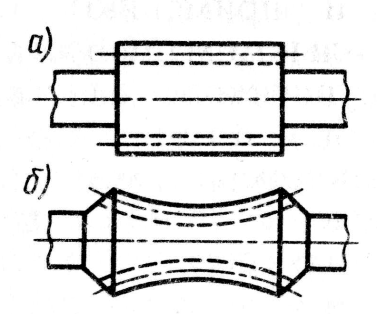
Расчет на прочность план.передач. Для расчета прочности зубьев планетарных передач используют те же формулы, что и при расчете простых передач. Расчет выполняют для каждого зацепления. Так как силы и модули внутреннего и наружного зацепления одинаковы (см. рис.2), а внутренне зацепление по своим свойствам прочнее наружного, то при одинаковых материалах достаточно рассчитывать только зацепление колес При расчете на изгиб применяют формулу При расчете по контактным напряжениям необходимо учесть число сателлитов Для планетарных передач рекомендуют
Выбор числа зубьев. Выбор числа зубьев связан с кинематическим расчетом и обычно предшествует расчету на прочность. При заданном передаточном отношении Условия соосности
Условие симметричного размещения сателлитов требует, чтобы Условие соседства предусматривает наличие гарантированного зазора между сателлитами
или
Червячные передачи
Общие сведения
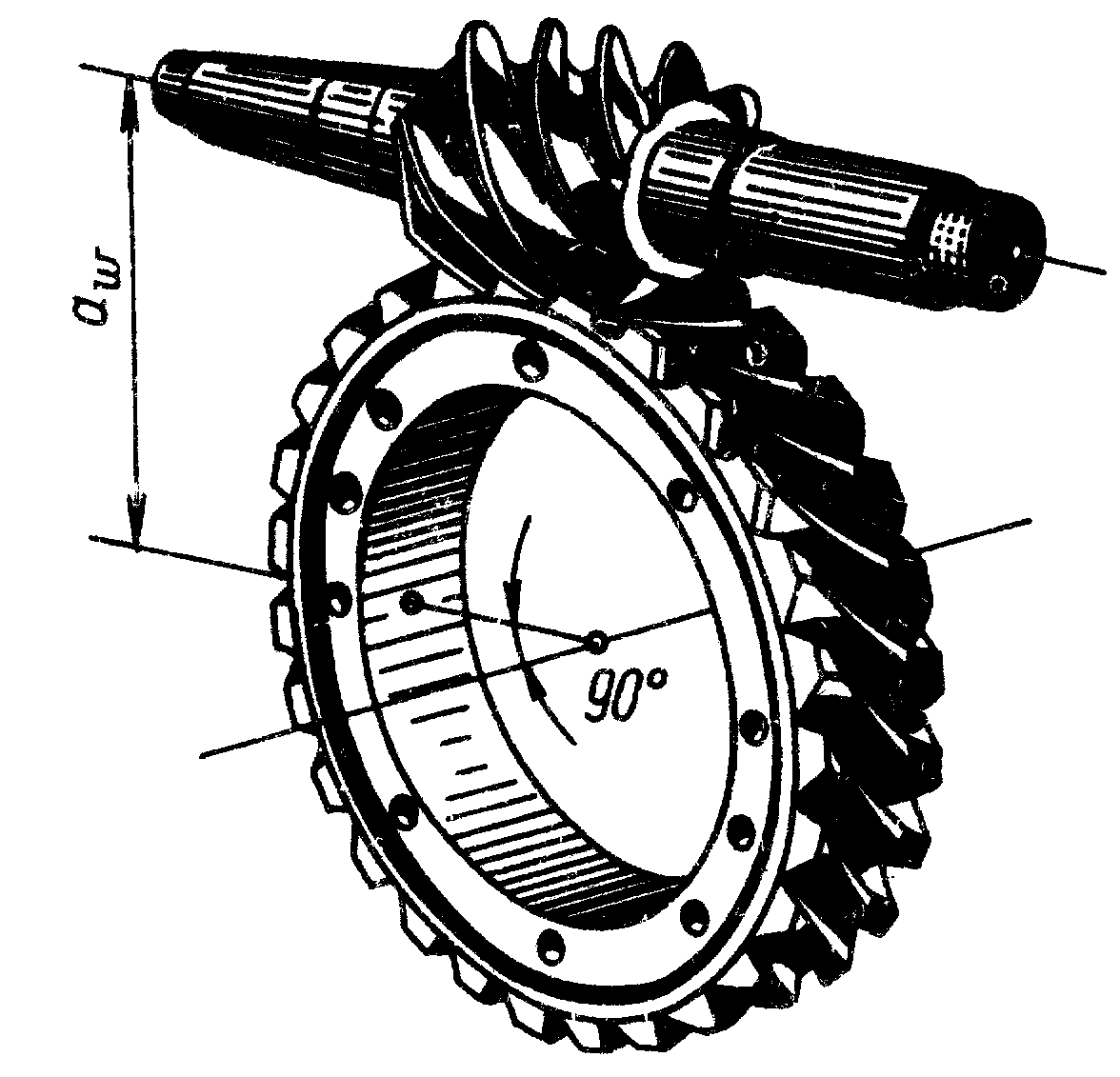
Червячная передача – это механизм для передачи вращения зацеплением с непосредственным контактом витков червяка и зубьев червячного колеса (рис.1).
Рис.1
Червяк – это винт с трапециидальной или близкой к ней по форме резьбой. Червячное колесо является косозубым зубчатым колесом с зубьями особой дуговой формы. Такая форма зубьев обеспечивает увеличение длины и прочности зубьев на изгиб. Червячные передачи применяют при необходимости передачи движения между перекрещивающимися валами. Угол перекрещивания обычно равен Достоинства червячных передач: 1) возможность получения большого передаточного числа в одной ступени; 2) плавность и малошумность в работе; 3) повышенная кинематическая точность; 4) возможность обеспечения самоторможения. Недостатки червячных передач: 1) низкий КПД; 2) необходимость изготовления зубьев колеса из дорогих антифрикционных материалов; 3) повышенные требования к точ6ности сборки, необходимость регулировки; 4) необходимость специальных мер по интенсификации теплоотвода. Указанные недостатки ограничивают мощность червячных передач (обычно до Червячные передачи применяют в станках, автомобилях, подъемно - транспортных машинах и других машинах.
Геометрические и кинематические параметры В червячной передаче различают диаметры начальных и делительных цилиндров (рис.2):
Рис.2 Рис.3
По форме тела червяки разделяют на цилиндрические (рис 3, а) и глобоидные ( рис. 3, б). По форме профиля резьбы – с прямолинейным (рис 4, а) и криволинейным (рис. 4 ,б) в осевом сечении. Наиболее распространены цилиндрические червяки. Цилиндрические червяки бывают видов: архимедов червяк, теоретический торцовый профиль которого – архимедова спираль; эвольвентный червяк, теоретический торцовый профиль которого – эвольвента. Архимедов червяк можно нарезать на обычных токарных или резьбофрезерных станках. Поэтому их широко применяют. С целью повышения работоспособности стали применять шлифованные высокотвердые червяки. Для шлифования архимедовых червяков требуются специальные шлифовальные круги фасонного профиля. Поэтому архимедовы червяки изготовляют в основном с нешлифованными витками при
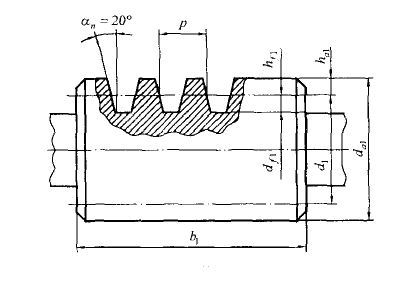
Рис.4 Геометрические параметры червяка
В червячных передачах угол профиля Делительный диаметр червяка принимается кратным модулю:
где Угол подъема витка червяка на делительном диаметре
Диаметры вершин и впадин:
Длина при числе витков
при числе витков
Примечание. Для шлифуемых и фрезеруемых червяков полученную величину b1 следует увеличить на 25 мм – при m < 10 мм; на 35…40 мм – при m = 10…16 мм.
Червячные колеса. Минимальное число зубьев червячных колес в силовых передачах
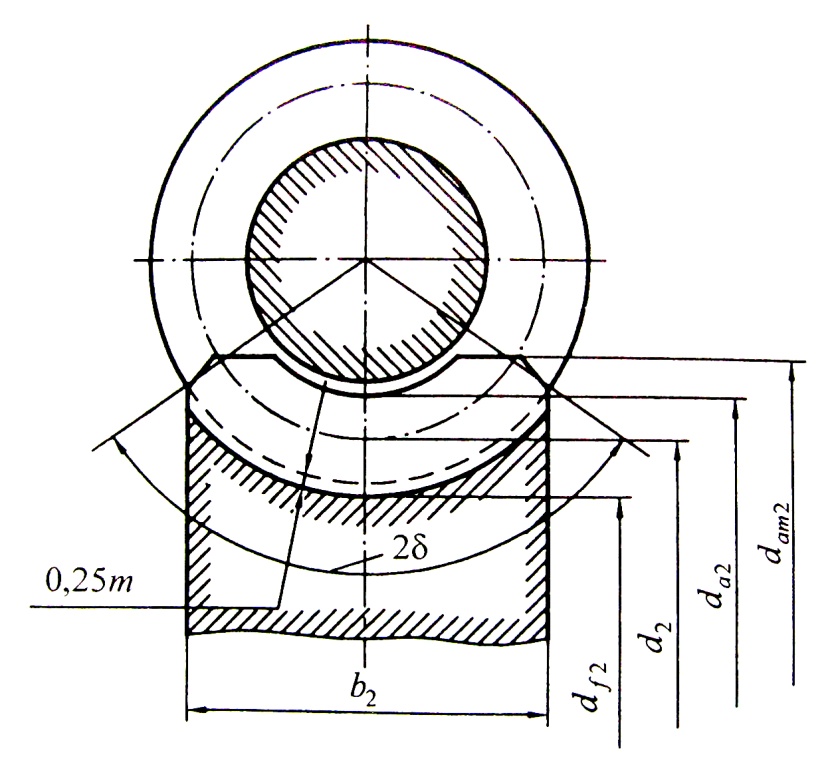
Рис. 5 Геометрические параметры червячного колеса
Ширина колеса
Наибольший диаметр колеса можно определить по формуле
где Силы в зацеплении В червячном зацеплении (рис.8) действуют: окружная сила червяка
окружная сила колеса
радиальная сила
сила нормальная
Вращающие моменты на валах червяка и червячного колеса связаны зависимостью:
Рис.8 Силы, действующие в червячном зацеплении
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 560. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
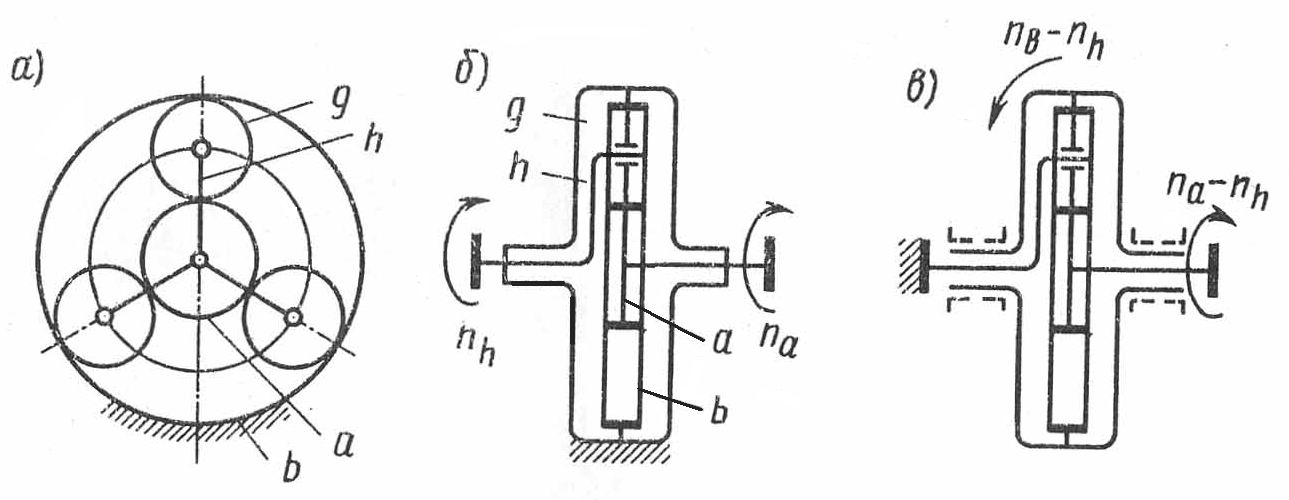 Рис 6.1
Рис 6.1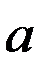 с наружными зубьями, центрального колеса
с наружными зубьями, центрального колеса 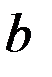 с внутренними зубьями, водила
с внутренними зубьями, водила 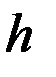 и сателлитов
и сателлитов 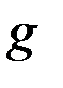 . Сателлиты вращаются вокруг своих осей и вместе с осью вокруг центрального колеса., При неподвижном колесе
. Сателлиты вращаются вокруг своих осей и вместе с осью вокруг центрального колеса., При неподвижном колесе 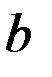 (рис.1,б) движение может передаваться от
(рис.1,б) движение может передаваться от  меньшие габариты и масса по сравнению с обычными зубчатыми передачами;
меньшие габариты и масса по сравнению с обычными зубчатыми передачами; ) возможность получения больших передаточных чисел (до 1000 и больше);
) возможность получения больших передаточных чисел (до 1000 и больше); широкие кинематические возможности (планетарную передачу можно использовать как редуктор, коробку скоростей и дифференциальный механизм);
широкие кинематические возможности (планетарную передачу можно использовать как редуктор, коробку скоростей и дифференциальный механизм); малые нагрузки на опоры, т.к. при симметричном расположении сателлитов силы в передаче взаимно уравновешиваются.
малые нагрузки на опоры, т.к. при симметричном расположении сателлитов силы в передаче взаимно уравновешиваются. повышенные требования к точности изготовления и сборки конструкции;
повышенные требования к точности изготовления и сборки конструкции; большое число подшипников качения.
большое число подшипников качения.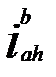 . Нижние индексы – направление передачи движения, верхний – неподвижное звено, относительно которого рассматривается движение.
. Нижние индексы – направление передачи движения, верхний – неподвижное звено, относительно которого рассматривается движение.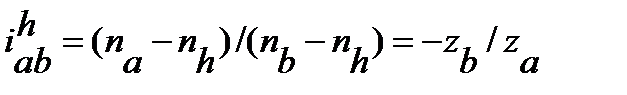
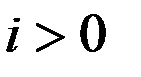 вращение ведущего и ведомого звена происходит в одном направлении; при
вращение ведущего и ведомого звена происходит в одном направлении; при 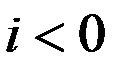 вращение звеньев противоположное.
вращение звеньев противоположное.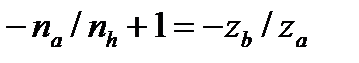
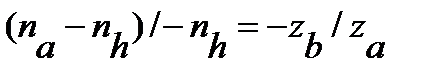
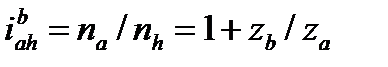
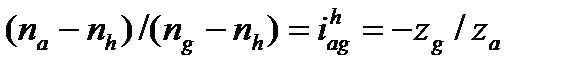 (6.3)
(6.3) 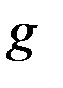 .
.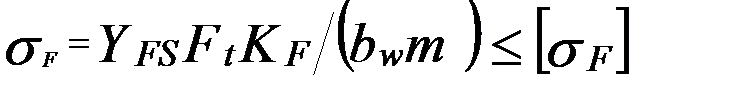 (6.11)
(6.11) 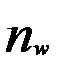 и коэффициент
и коэффициент 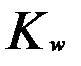 . Например, диаметр меньшего колеса пары определим по формуле
. Например, диаметр меньшего колеса пары определим по формуле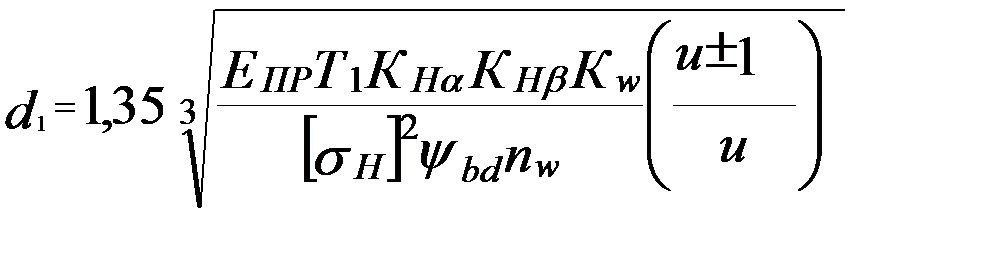 (6.12)
(6.12) 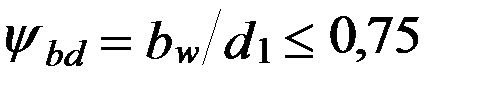 (6.13)
(6.13) 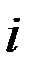 числа зубьев определяют предварительно с помощью формул (6.2),(6.10). Полученные значения уточняют по условиям собираемости планетарной передачи. Для передачи (рис.6.1) эти условия следующие
числа зубьев определяют предварительно с помощью формул (6.2),(6.10). Полученные значения уточняют по условиям собираемости планетарной передачи. Для передачи (рис.6.1) эти условия следующие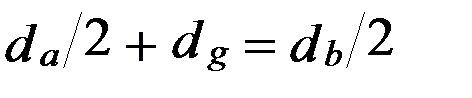 или
или 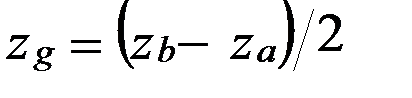 (6.14)
(6.14) 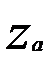 и
и 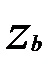 были кратны числу сателлитов
были кратны числу сателлитов 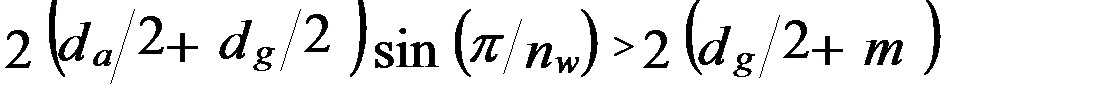 (6.15)
(6.15) 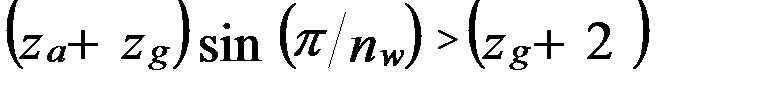
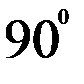 .
.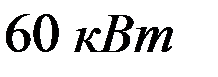 ).
). ,
, 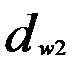 – начальные диаметры червяка и колеса;
– начальные диаметры червяка и колеса; 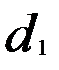 ,
, 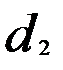 – делительные диаметры червяка и колеса. В передачах без смещения
– делительные диаметры червяка и колеса. В передачах без смещения 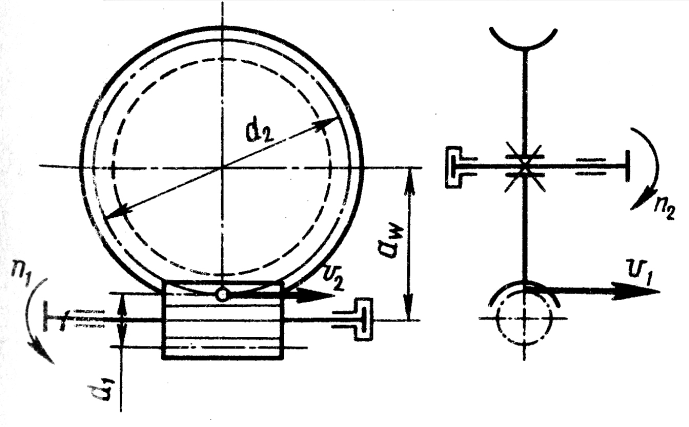
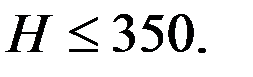
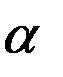 принимают равным
принимают равным 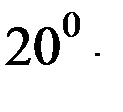 . Расстояние между одноименными точками боковых сторон смежных витков червяка называют шагом
. Расстояние между одноименными точками боковых сторон смежных витков червяка называют шагом 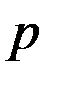 червяка. . Отношение
червяка. . Отношение 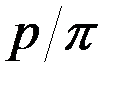 называют осевым модулем
называют осевым модулем 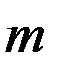 . Резьба червяка может быть однозаходной или многозаходной. Число заходов червяка обозначают
. Резьба червяка может быть однозаходной или многозаходной. Число заходов червяка обозначают 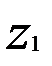 . По стандарту,
. По стандарту, 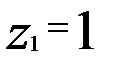 ;
; 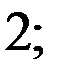
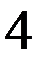 . Рекомендуют:
. Рекомендуют: 
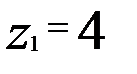 при передаточном отношении
при передаточном отношении 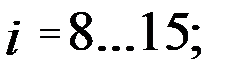
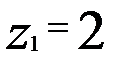 при
при 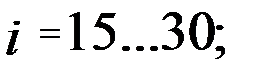
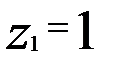 при
при 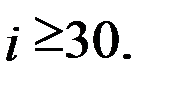
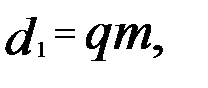 (1)
(1)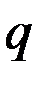 – коэффициент диаметра червяка. Значения
– коэффициент диаметра червяка. Значения 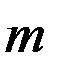 и
и 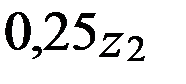 .
.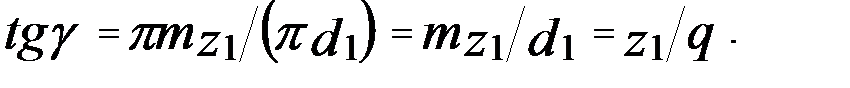 (2)
(2)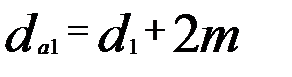 ;
; 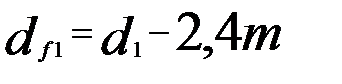 . (3)
. (3)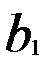 нарезанной части червяка:
нарезанной части червяка: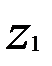 =
= 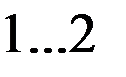
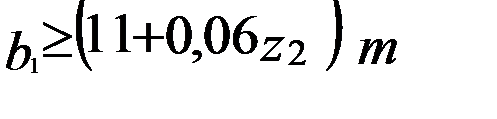 ;
;
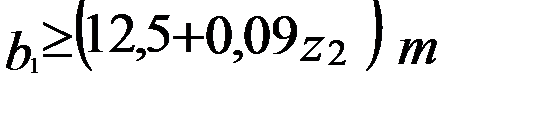 .
.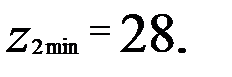 Наиболее желательно для силовых передач
Наиболее желательно для силовых передач 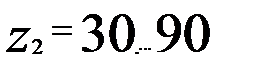 . Геометрические параметры червячного колеса, нарезанного без смешения (рис. 5), равны:
. Геометрические параметры червячного колеса, нарезанного без смешения (рис. 5), равны: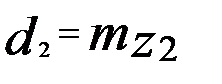 ;
; 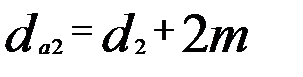 ;
; 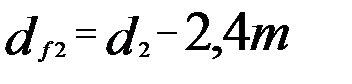 ;
;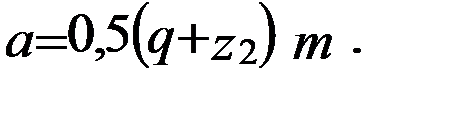 (4)
(4)
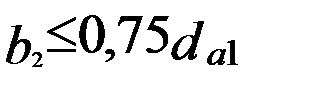 (при
(при 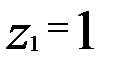 или
или 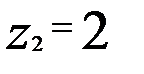 ),
), 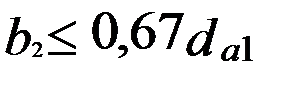 (при
(при 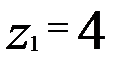 ).
).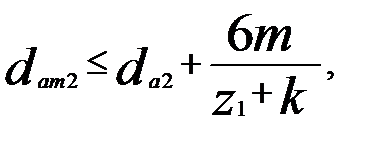 (5)
(5)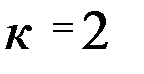 для архимедовых и эвольвентных червяков.
для архимедовых и эвольвентных червяков.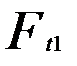 , равная осевой силе колеса
, равная осевой силе колеса 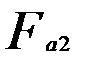 ,
,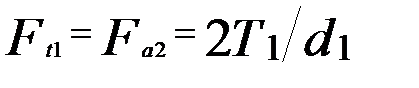 ; (11)
; (11)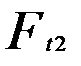 , равная осевой силе червяка
, равная осевой силе червяка 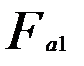 ,
,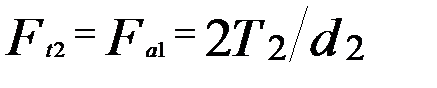 ; (12)
; (12)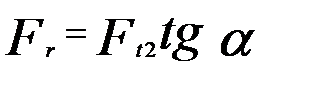 ; (13)
; (13)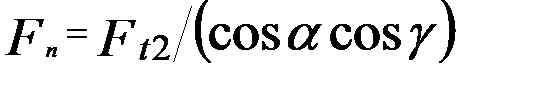 . (14)
. (14) 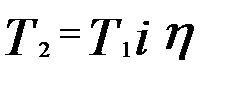 . (15)
. (15)