
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Отклонения генеральной совокупности по данным выборки.На практике иногда необходимо найти неизвестное среднее квад-ратическое отклонение генеральной совокупности σ0 по среднему квадратическому отклонению s малой выборки, когда ее объем n < 30. Для малых выборок s вычисляется по формуле
где в знаменателе берется (п - 1), для того чтобы компенсировать систематическую ошибку, возникающую при оценке σ0 по s при малом числе n. Эта задача сводится к определению вероятности α приближенного равенства
Если случайная величина х в генеральной совокупности подчинена нормальному закону распределения, то вероятность α уравнения (13)
приближенного равенства
Дифференциальная функция (плотность вероятности)
Для вычисления вероятности α, полагая, что s - ε > 0, преобразуем находящееся в скобках уравнения (13) неравенство
Умножим полученное неравенство на положительное число
Обозначив
Вероятность этого неравенства равна интегралу
Но левая часть этого уравнения есть преобразованное выражение вероятности
Следовательно, можно написать
или
Значения интеграла L(qs, k)приведены в табл. П.5 приложения. Таким образом, по таблице П.3 приложения можно определить вероятность α того, что отклонения σ0 от s не превосходят ε = qss.
Необходимо заметить, что если s < ε, то исходное неравенство для σ0 
надо заменить неравенством
так как величина σ0 должна быть положительной. В этом случае неравенство для χ примет вид
и вероятность его будет определяться интегралом
Значения этого интеграла также приведены в табл. П.3 приложения. При помощи этой таблицы значений вероятностей L(qs, k) можно решать задачи трех типов: 1) по заданной точности ε = qss и объеме выборки n определить вероятность α приближенного равенства 2) по заданной вероятности α приближенного равенства 3) по заданной точности ε и вероятности α приближенного равенства
Пример 4. По выборке объема п = 15 вычислено среднее квадратическое отклонение s = 0,6. Определить вероятность α приближенного равенства Вычислим значение qs, используя формулу ε = qss. Получим Следовательно, среднее квадратическое отклонение
Пример 5.Определить точность ε приближенного равенства
По таблице П.3 приложения для k = п - 1 = 14 и α = 0,96 находим qs = 0,5. По формуле ε = qss находим ε = 0,5·0,12= 0,06. Следовательно,
σ0 = s ± ε = 0,12±0,06.
Пример 6.Определить объем выборки n, при котором s будет отличаться от σ0 на ±0,2s с вероятностью α = 0,96.
Учитывая, что ε = qss = 0,2s, находим qs = 0,2.
По таблице П.3 при qs = 0,2 и α = 0,96 находим k = 60. Но k = n - 1, следовательно, n = 61.
Оценка параметров нормального распределения |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 369. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
, , точность которого равна ε:
, точность которого равна ε: . (13)
. (13)
 -распределение
-распределение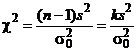 .
. при χ > 0.
при χ > 0. следующим образом:
следующим образом: .
.
 .
. и
и  , получим
, получим или
или  .
. . (14)
. (14) (15)
(15)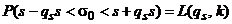 . (16)
. (16)
 ,
,
 .
. ;
;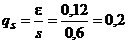 . По таблице П.3 для
. По таблице П.3 для 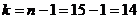 и
и  находим α = 0,701.
находим α = 0,701. случайной переменной генеральной совокупности с вероятностью α = 0,701 находится в интервале 0,6 - 0,12 < σ0 < 0,6 + 0,12, т. е. 0,48 < σ0 < 0,72
случайной переменной генеральной совокупности с вероятностью α = 0,701 находится в интервале 0,6 - 0,12 < σ0 < 0,6 + 0,12, т. е. 0,48 < σ0 < 0,72