
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Распределения случайной величины
Для установления закона распределения генеральной совокупности по большой выборке из нее пользуются рядом критериев, из которых наибольшее практическое применение имеют критерий λ А. Н. Колмогорова и критерий Критерий λ. Этот критерий дает достаточно точные результаты даже при объеме выборок, состоящих из нескольких десятков членов и прост для вычислений. Для вычисления величины λ необходимо предварительно определить значения эмпирической Fэ(х) и теоретической F(х) интегральной функции предполагаемого закона распределения для каждого наблюденного значения случайной величины х. Затем по максимальной разности значений этих функций определяется λ при помощи следующей формулы:
Так как
Накопленной частотой любого m-го значения xi называется сумма частот всех предшествующих значений xi, включая и частоту самого xi, т. е.
где m — число значений хi; fi - частота i-го значения х. Академик А. Н. Колмогоров доказал, что для непрерывных случайных величин
где Функция K(λ) табулирована Н. В. Смирновым и при помощи таблицы значений K(λ) составлена таблица значений P(λ), которая приведена в приложении (таблица П6). По вычисленному по формуле (4) или (5) значению λ по таблице П5 приложения определяют P(λ). Если вероятность P(λ) окажется очень малой, практически, когда P(λ) ≤ 0,05, то расхождение между F(x) и Fэ(х) считается существенным, а не случайным и гипотеза о предполагаемом законе распределения величины x бракуется. Если же вероятность P(λ) будет достаточно большой (практически, когда P(λ) > 0,05), то гипотеза принимается.  Использование критерия λ предполагает непрерывность Для удобства вычисления критерия λ составляют вспомогательную таблицу, в которой накопленные частоты функции
Таблица 6. Данные для вычисления критерия l
Критерий Критерий
где m– число интервалов сравниваемых частот; Для удобства вычисления
Таблица 7. Вспомогательная таблица для вычисления критерия
Далее вычисляют число степеней свободы k по формуле k = m - p - 1, где m — число сравниваемых частот (разрядов); p — число параметров теоретического распределения. Для величины k найден закон распределения, по которому вычислены вероятности Если
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 343. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||
 Пирсона.
Пирсона. .
.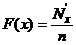 и
и  , где
, где  и
и  - накопленные теоретические и эмпирические частоты, а n — объем выборки, то вместо вышеприведенной формулы можно пользоваться следующей формулой:
- накопленные теоретические и эмпирические частоты, а n — объем выборки, то вместо вышеприведенной формулы можно пользоваться следующей формулой: . (5)
. (5) (6)
(6) ,
, . Для больших n и любом l > 0
. Для больших n и любом l > 0  .
. и, кроме того, предполагается, что эмпирическая функция
и, кроме того, предполагается, что эмпирическая функция  построена по не сгруппированным в интервалы значениям случайной величины х. Однако в случае, когда интервалы группировки достаточно малы, критерий λ дает, хотя и приближенную, но вполне приемлемую для практических целей оценку близости эмпирического распределения к теоретическому.
построена по не сгруппированным в интервалы значениям случайной величины х. Однако в случае, когда интервалы группировки достаточно малы, критерий λ дает, хотя и приближенную, но вполне приемлемую для практических целей оценку близости эмпирического распределения к теоретическому.
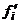



 , (7)
, (7) – эмпирическая частота i-го интервала значений x;
– эмпирическая частота i-го интервала значений x; 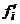 – теоретическая частота i-го интервала значений х.
– теоретическая частота i-го интервала значений х.




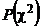 для различных значений
для различных значений  и k. Значения
и k. Значения  , гипотеза о законе распределения должна быть забракована. Если
, гипотеза о законе распределения должна быть забракована. Если  , то гипотеза принимается.
, то гипотеза принимается.