
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Численное интегрирование функции одной переменной5.1. Квадратурные формулы Пусть требуется вычислить определенный интеграл где f (x) – интегрируемая на промежутке [a, b] функция, заданная таблично в узлах сетки i = 0, 1, 2,….,n. Для приближенного вычисления определенного интеграла I используют квадратурные формулы вида I »
5.2. Квадратурная формула Симпсона Предполагается, что промежуток [a, b] разбит на четное число n = 2m равных промежутков длины h. На каждом из промежутков [xi, xi+2] для i = 0, 2, 4,…, (2m – 2) функцию f (x) заменим на интерполяционный полином 2-го порядка gi(x) = aix2 + bix + ci, которому графически соответствует парабола, проходящая через 3 точки: (xi, f(xi)), (xi+1, f(xi+1)) и (xi+2, f(xi+2)). Интеграл от функции gi(x) по промежутку [xi, xi+2] даст приближенное значение интеграла
В этой формуле:
Решение обыкновенных дифференциальных уравнений 1-го порядка методом Рунге-Кутты Пусть требуется найти на промежутке [a, b] решение задачи Коши для обыкновенного дифференциального уравнения 1-го порядка:  y¢ = f (x, y), y(x0) = y0, где x0, y0 – заданные числа. Предполагается, что решение y(x) задачи Коши существует и единственно. Приближенное решение дифференциального уравнения 1-го порядка находят в узлах одномерной сетки Опишем так называемый метод Рунге-Кутты 4-го порядка, наиболее широко используемый на практике. Зададим на промежутке [a, b] равномерную сетку с шагом yi+1 = yi + где величины k1, k2, k3, k4 для каждого yi+1 вычисляют по формулам:
Говорят, что некоторый численный метод решения задачи Коши имеет порядок точности k > 0, если существует такое число q > 0, при котором выполнено условие: ôyi – y (xi)ô£ q hk, i = 0, 1,...,n, где h – шаг сетки, y (xi) –значение точного решения уравнения в точке xi, а yi – приближенное значение решения в точке xi, полученное данным методом. Метод Рунге-Кутты 4-го порядка имеет четвертый порядок точности.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 179. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
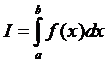
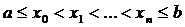 , т.е. известны ее значения f (xi) для
, т.е. известны ее значения f (xi) для , где коэффициенты αi выбирают тем или иным методом. Погрешность квадратурной формулы
, где коэффициенты αi выбирают тем или иным методом. Погрешность квадратурной формулы  зависит от выбора коэффициентов αi, разбиения промежутка [a, b] и погрешности вычислений, в которую входит и погрешность вычисления значений функции f (xi) в узлах сетки.
зависит от выбора коэффициентов αi, разбиения промежутка [a, b] и погрешности вычислений, в которую входит и погрешность вычисления значений функции f (xi) в узлах сетки. , а сумма этих интегралов по всем участкам даст приближенное значение интеграла
, а сумма этих интегралов по всем участкам даст приближенное значение интеграла  . Соответствующая квадратурная формула называется квадратурной формулой парабол, или квадратурной формулой Симпсона и имеет следующий вид:
. Соответствующая квадратурная формула называется квадратурной формулой парабол, или квадратурной формулой Симпсона и имеет следующий вид: , или
, или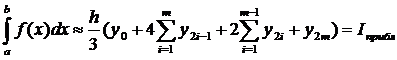 . (15)
. (15) – шаг сетки, т.е. длина промежутка [xi, xi+1] для i = 0, 1, 2,…, 2m– 1; yi = f (xi) – значения функции в узлах сетки (для i = 0, 1, 2,…, 2m).
– шаг сетки, т.е. длина промежутка [xi, xi+1] для i = 0, 1, 2,…, 2m– 1; yi = f (xi) – значения функции в узлах сетки (для i = 0, 1, 2,…, 2m). , т.е. вычисляют значения yi
, т.е. вычисляют значения yi  y(xi) для i = 0, 1,…., n. Для численного решения задачи Коши используют разностные методы и методы Рунге – Кутты (Рунге-Кутта).
y(xi) для i = 0, 1,…., n. Для численного решения задачи Коши используют разностные методы и методы Рунге – Кутты (Рунге-Кутта). , тогда xi = x0 + ih для i = 0, 1,….,n. Значение y(x0) = y0 задано в начальном условии задачи. Каждое следующее значение yi+1
, тогда xi = x0 + ih для i = 0, 1,….,n. Значение y(x0) = y0 задано в начальном условии задачи. Каждое следующее значение yi+1  (k1 + 2k2 + 2k3 + k4), (16)
(k1 + 2k2 + 2k3 + k4), (16) (17)
(17)