
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение нелинейных уравнений2.1. Изоляция корней Пусть требуется найти корни (решения) уравнения f (x) = 0 (5), где f (x) – нелинейная функция. В общем случае можно говорить лишь о приближенном вычислении корней уравнения (5), т.е. о получении такого значения аргумента, при котором f (x) » 0. Принято считать, что точное решение x* этого уравнения получено с точностью ε, если для полученного приближенного решения x выполнено условие Если непрерывная функция f (x) является знакопеременной в области определения, то уравнение (5) имеет конечное или бесконечное количество корней. Каждый из корней получают, используя численные методы, после процедуры отделения корней. Отделить корень уравнения (5) – значит найти такой интервал (a, b), в котором содержится корень уравнения, причем только один. Известно, что если на концах некоторого промежутка [a, b] непрерывная функция f (x) имеет разные знаки, т.е. Процедура отделения корней может быть осуществлена графически (построением графика функции f (x)) или с помощью проверки знака функции на некотором множестве значений x, например, на множестве равноотстоящих точек на оси абсцисс. 2.2. Уточнение корней уравнения методом деления отрезка пополам Пусть требуется решить уравнение (5) с заданной точностью ε. Известен промежуток изоляции корня x* – промежуток [a, b], на концах которого непрерывная функция f (x) имеет разные знаки, а внутри этого промежутка производная Процедура уточнения корня заключается в построении последовательности точек x0, x1, x2, ….. xk,…., такой, что 
Опишем метод уточнения корня, называемый методом деления отрезка пополам, или методом дихотомии, или методом бисекции. Иногда этот метод называют еще методом проб. Уточнение корня методом деления отрезка пополам осуществляется в следующем порядке: 1) вводим обозначении: а0 = a, b0 = b; 2) вычисляем 3) из двух интервалов (а0, x0) и (x0, b0) выбираем тот, на концах которого f (x) имеет разные знаки, и обозначаем концы этого интервала a1, b1; 4) вычисляем 5) из двух интервалов (а1, x1) и (x1, b1) выбираем тот, на концах которого f (x) имеет разные знаки, и обозначаем концы этого интервала a2, b2; 6) вычисляем и так далее, пока не будет выполнено условие Последовательность {xk}, полученная методом деления отрезка пополам, сходится к точному решению х*, если функция f (x) непрерывна на [a, b]. Описание алгоритма метода. 1. Для k = 0 выполняем:
2. Увеличиваем номер шага k := k + 1, выполняем вычисления:
3. Проверяем условие
Если условие не выполняется, переходим к пункту 2, если условие выполняется, то процесс закончен. Получаем ответ: |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 175. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. , а внутри этого промежутка производная
, а внутри этого промежутка производная  знак не меняет, то в интервале (a, b) существует корень уравнения (5), причем только один.
знак не меняет, то в интервале (a, b) существует корень уравнения (5), причем только один. . Процесс вычисления заканчивается, когда получено xk, удовлетворяющее условию
. Процесс вычисления заканчивается, когда получено xk, удовлетворяющее условию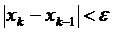 . (6)
. (6) ;
; ;
; ,
, , – тогда приближенное значение корня
, – тогда приближенное значение корня  будет удовлетворять условию (6), т.е. решением уравнения будет число
будет удовлетворять условию (6), т.е. решением уравнения будет число  .
. . (7)
. (7) (8.1)
(8.1) (8.2)
(8.2)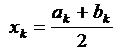 . (8.3)
. (8.3) . (9)
. (9) .
.