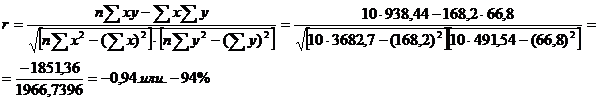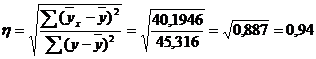Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Зависимость среднесуточного производства продукции от простоев
Найдем параметры теоретической линии регрессии -
Получаем значение параметров:
Теоретическая линия регрессии равна:
Значение теоретической линии регрессии такие: для:
Надо отметить, что при выборе вида теоретической линии регрессии можно не только воспользоваться графическими изображениями эмпирических данных и эмпирическим путем определять вид направления зависимости, но и можно использовать метод конечных разностей между последующими и предыдущими вариантами.  Так если первые разности между последующими и предыдущими вариантами одинаковы, т.е. Если вторые разности вариантов рядов распределения одинаковые, т.е. Для определения параметров a, b и с решаются следующие уравнения нормальных уравнений: Для несгруппированных данных:
Для сгруппированных данных:
Надо отметить, что криволинейную тенденцию во многих случаях можно аппроксимировать при помощи параболы более высокого порядка:
Существуют и другие методы при выборе формы уравнения[11].
Показатели тесноты связи: коэффициент корреляции, эмпирическое корреляционное отношение (для сгруппированных данных), теоретическое корреляционное отношение (для сгруппированных и несгруппированных данных). Показатели тесноты связи показывают, какой удельный вес занимает признак-фактор «x» среди всех факторов, влияющих на признак-результат – «y». Они отвечают на вопрос: насколько необходимо изучение данной связи между признаками и целесообразности её практического применения, а также позволяет выявить наиболее значимые факторы, которые являются решающими при формировании результативного признака. Коэффициент корреляции[12] r является показателем тесноты связи. Он измеряется так же и направление зависимости. Коэффициент корреляции равен: Для сгруппированных данных:
Для не сгруппированных данных:
Если коэффициент корреляции принимает значение: - от 0 - от 0,4 - от 0,6 - от 0,8 Кроме того, коэффициент корреляции, как указано выше, показывает направление зависимости. Если коэффициент корреляции принимает значение: от -1 до 0, то связь обратная. Если коэффициент корреляции принимает значение от 0 до 1 – то связь прямая. Если Коэффициент корреляции применяется только для прямолинейной связи. Эмпирическое корреляционное отношение – ρ, которое является универсальным показателем тесноты связи, так как применяется для прямо или криволинейной зависимости. Но в отличие от коэффициента корреляции, этот показатель не показывает направления связи. Он применяется только для сгруппированных данных. Эмпирическое корреляционное отношение равно:
Степень тесноты связи у эмпирического корреляционного отношения такая же как у коэффициента корреляции. При прямолинейной зависимости эмпирическое корреляционное отношение всегда будет немножко больше, чем абсолютное значение коэффициента корреляции. Теоретическое корреляционное отношение – Для сгруппированных данных:
Расчет: Для несгруппированных данных:
Поэтому, для несгруппированных данных теоретическое корреляционное отношение примет такой вид:
Теоретическое корреляционное отношение так же, как и эмпирическое корреляционное отношение является универсальным показателем, так как применяется при прямолинейной и криволинейной зависимости. Степень тесноты связи у теоретического корреляционного отношения такая же как у коэффициента корреляции и у эмпирического корреляционного отношения. При прямолинейной зависимости теоретическое корреляционное отношение будет всегда равно коэффициенту корреляции. А эмпирическое корреляционное отношение всегда будет незначительно больше теоретического корреляционного отношения. Рассмотрим показатели тесноты связи для сгруппированных данных. Для расчета воспользуемся корреляционной таблицей зависимости товарной продукции «y» от производительности труда «х» (см. табл. 14). Коэффициент корреляции равен:
Эмпирическое корреляционное отношение равно:
Таким образом, связь между производительностью труда и товарной продукцией будет тесная, корреляционная; на 66% изменение товарной продукции зависит от изменения производительности труда. Теоретическое корреляционное отношение равно:
Таким образом, связь между производительностью труда и товарной продукцией будет тесная, корреляционная; на 63,5% изменение товарной продукции зависит от изменения производительности труда. Мы видим, что Далее рассчитаем показатели тесноты связи для несгруппированных данных на основе таблицы … Коэффициент корреляции равен:
Связь между среднесуточным производством продукции и простоями будет обратная, довольно-таки тесная; т.е. на 94% среднесуточное производство зависит от снижения простоев, а на 6 % от других факторов. Теоретическое корреляционное отношение равно:
Таким образом, связь между среднесуточным производством продукции и простоями будет довольно таки тесная и на 94% среднесуточное производство зависит от простоев.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 383. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
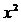
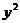
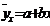
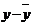
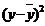
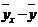
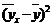
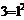
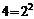
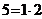
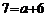
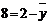
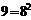
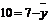
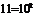
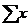 =168,2
=168,2
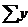 =66,8
=66,8
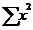 =3682,7
=3682,7
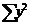 =491,54
=491,54
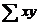 =938,44
=938,44
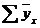 =66,8
=66,8
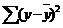 =45,316
=45,316
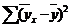 =40,1946
=40,1946
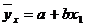 , при помощи решение системы нормальных уравнений.
, при помощи решение системы нормальных уравнений.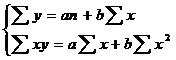
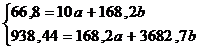
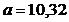
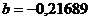 - коэффициент регрессии показывает, что с ростом простоев на 1% к календарному времени работы среднесуточное производство продукции снизилось на 0,21689 тыс. шт. или на 216,89 шт.
- коэффициент регрессии показывает, что с ростом простоев на 1% к календарному времени работы среднесуточное производство продукции снизилось на 0,21689 тыс. шт. или на 216,89 шт.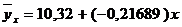
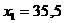
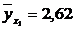
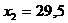
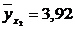
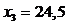
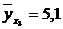
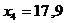
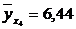
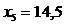
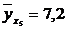
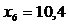
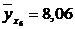
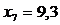
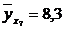
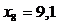
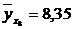
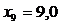
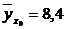

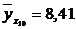
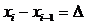 , то теоретическая линия регрессии выражается линейным уравнением
, то теоретическая линия регрессии выражается линейным уравнением 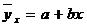 .
.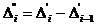 , то теоретическая линия регрессии выражается параболой второго порядка
, то теоретическая линия регрессии выражается параболой второго порядка 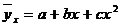 . Данное уравнения позволяет выявить не только скорость изменения вариантов «х», которую отражает коэффициент регрессии – «b», но и ускорение, которое учитывает параметр «с».
. Данное уравнения позволяет выявить не только скорость изменения вариантов «х», которую отражает коэффициент регрессии – «b», но и ускорение, которое учитывает параметр «с».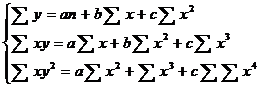
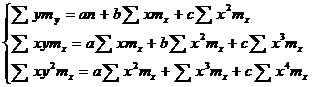
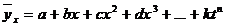
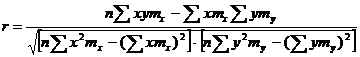
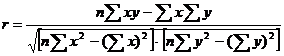
 до 0,45, то связь между х и y – слабая
до 0,45, то связь между х и y – слабая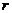 = 0, то связь отсутствует, если
= 0, то связь отсутствует, если 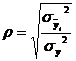 , где
, где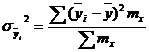 - дисперсия по эмпирической линии регрессии
- дисперсия по эмпирической линии регрессии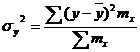 или
или 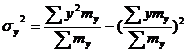 - общая дисперсия
- общая дисперсия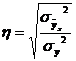 , где:
, где: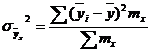 - дисперсия по теоретической линии регрессии
- дисперсия по теоретической линии регрессии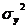 общая дисперсия см. выше
общая дисперсия см. выше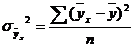 - дисперсия по теоретической линии регрессии
- дисперсия по теоретической линии регрессии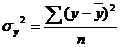 - общая дисперсия
- общая дисперсия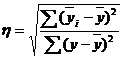
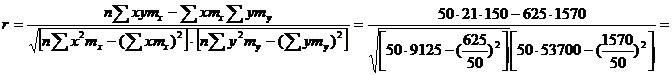
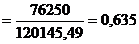 или 63,5%, т.е. связь между производительностью труда и товарной продукцией будет тесная, прямолинейная корреляционная, на 63,5% изменения товарной продукции зависят от изменения производительности труда, и на 36,5% - от других факторов (учтенных и не учтенных).
или 63,5%, т.е. связь между производительностью труда и товарной продукцией будет тесная, прямолинейная корреляционная, на 63,5% изменения товарной продукции зависят от изменения производительности труда, и на 36,5% - от других факторов (учтенных и не учтенных).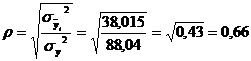 , где
, где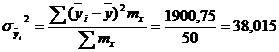
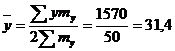
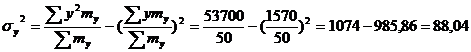
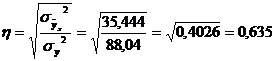 или 63,5%
или 63,5%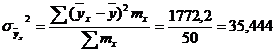
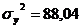 [13]
[13]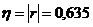 .
.