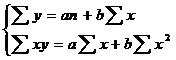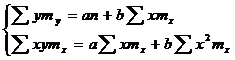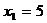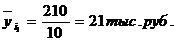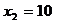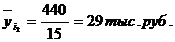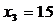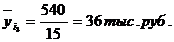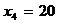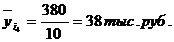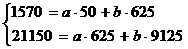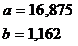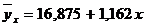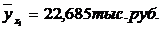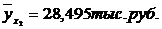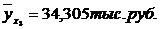Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Показатели направления зависимости: эмпирическая линия регрессии (для сгруппированных данных), теоретическая линия регрессии.Эмпирическая линия регрессии показывает как в среднем изменяется признак-результат «y» в зависимости от изменения признака-фактора «х» при условии неизменности всех остальных факторов. Эмпирическая линия регрессии применяется только для сгруппированных данных, она равна:
Втором показателем направления зависимость является теоретическая линия регрессии, которая показывает как в среднем изменяется признак-результат «y» в зависимости от изменения признака-фактора «х» при полном исключении всех остальных факторов. Теоретическая линия регрессии строится по результатам математическим функциям в зависимости от исходных данных[10]. Теоретическая линия регрессии по прямой равна:
а – параметр, который показывает высоту графика и экономического смысла не имеет; b – коэффициент регрессии, который показывает, на сколько в среднем изменится признак-результат «y» при увеличении признака-фактора «х» на единицу измерения (то есть параметр b изучает направление признака-результата). Для определения параметров (а и b) необходимо решить систему нормальных уравнений. Для несгруппированных данных:
Для сгруппированный данных:
Показатели направления зависимости для сгруппированных данных. Рассчитаем эти показатели для сгруппированных данных по данным корреляционной таблице. Значения эмпирической линии регрессии следующие: для для для для Нанесем эти значения на графики – на поле корреляции. Находим параметры (а и b) при помощи системы нормальных уравнений:
Получаем значение параметров:
Коэффициент регрессии b показывает, что с увеличением производительности на 1 руб./чел., товарная продукция вырастает на 1,162 тыс. руб.  Теоретическая линия регрессии равна:
Значение теоретической линии регрессии такие: для для для для Нанесем на рисунок теоретическую линию регрессии. Показатели направления зависимости для несгруппированных данных. Рассчитаем показатель направления зависимости – теоретическую линию регрессии для несгруппированных данных. Для этого на основании таблицы 15 определим направление зависимости среднесуточного производства продукции «y» (тыс. руб.) от «х» - простоев (в % к календарному времени работы). Таблица 15 |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 380. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
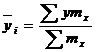
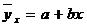 , где
, где