
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Точечные оценки параметров распределенияЧисловые характеристики всей генеральной совокупности называются параметрами. Так как всю генеральную совокупность изучить достаточно часто не представляется возможным, о параметрах судят по выборочным характеристикам. На основании выборочных данных можно получить лишь приближенное значение параметра, которое является его оценкой. Обозначим Многократные выборки одинакового объёма дадут различные значения параметра 1. Оценка 2. 3. Состоятельной называется оценка, которая при Репрезентативная выборка – это такая выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности. При достаточно большом значении объёма выборки нет разницы в выборе смещённой или несмещённой оценки параметра, при малом n необходимо рассматривать несмещённую оценку, поскольку выборка будет репрезентативной, то есть полностью представлять генеральную совокупность. Для выборки можно определить ряд числовых характеристик: выборочное среднее, выборочная дисперсия, выборочное среднеквадратическое отклонение, размах выборки, асимметрия, эксцесс.  Пусть статистическое распределение выборки объёма n имеет вид:
1) Выборочное среднее (обозначается
Выборочное среднее показывает среднее значение, вокруг которого группируются варианты. Свойства средней арифметической 1. 2. 3. 4. 5. 2) Выборочная дисперсия – это среднее арифметическое квадратов отклонений значений выборки от выборочной средней.
Выборочная дисперсия показывает меру разброса данных вокруг среднего значения. Она является состоятельной и смещённой оценкой дисперсии. Свойства средней арифметической 1. 2. 3. 4. Алгоритм расчёта выборочной дисперсии 1) Вычисляется объём выборки n; 2) Находится выборочная средняя 3) Определяется величина 4) Для оценки степени отклонения от среднего значения удобно иметь дело с величиной той же размерности, что и величина Х. Для этого вводится понятие выборочного среднеквадратического отклонения. 3) Выборочное среднеквадратической отклонение – это арифметическое значение корня квадратного из его дисперсии, т.е.
4) Размах выборки (обозначается
Для подробного описания особенностей распределения используют дополнительные характеристики – моменты распределения. Выяснение общего характера предполагает не только оценку степени его однородности, но и позволяет исследовать форму распределения. Средняя из k-х степеней отклонений вариант
При расчёте средних в качестве весов можно использовать частоты, относительные частоты или вероятности. При использовании в качестве весов частот или относительных частот моменты называются эмпирическими (обозначаются Эмпирический момент k-го порядка – это отношение суммы произведений k-х степеней отклонений вариант от постоянной величины
Практически используют моменты первых четырех порядков. Если Нормальное распределение является одним из самых распространённых в применениях математической статистики. Для оценки отклонения эмпирического распределения от нормального используются нормированные моменты.
Для облегчения расчётов можно воспользоваться соотношениями между начальными и центральными моментами:
Из математической статистики известно, что при увеличении объёма статистической совокупности Однородные совокупности описываются одновершинными распределениями. Многовершинность распределения свидетельствует о неоднородности изучаемой совокупности или о некачественном выполнении группировки. Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные. Распределение называется симметричным, если частоты любых 2-х вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Для характеристики асимметрии используют коэффициент асимметрии. При симметричном распределении варианты, равноудаленные от 5) Коэффициент асимметрии
В одновершинных распределениях величина этого показателя изменяется от –1 до +1. в симметричных распределениях – если – если – если
Рис. 5 Правосторонняя Рис. 6 Левосторонняя асимметрия асимметрия
6) Для нормального распределения
Кривые распределения, у которых Рассматривая формулы моментов, можно видеть, что начальный момент первого порядка представляет собой среднюю арифметическую и используется как показатель центра распределения. Центральный момент первого порядка (нулевое свойство средней арифметической) всегда равен нулю. Центральный момент второго порядка представляет собой дисперсию и служит основной мерой колеблемости признака. Центральный момент третьего порядка равен нулю в симметричном распределении и используется для определения показателя асимметрии. Центральный момент четвертого порядка применяется при вычислении показателя эксцесса. Начальные моменты второго, третьего и четвертого порядка, так же как и условные моменты, самостоятельного значения не имеют, а используются для упрощения вычислений центральных моментов. Пример решения задания 2 Задан вариационный ряд выборки. Найти: выборочное среднее, выборочную дисперсию, выборочное среднеквадратическое отклонение, размах выборки, асимметрию, эксцесс.
Решение Объём выборки: 1) Выборочное среднее:
2) Выборочная дисперсия:
3) Выборочное среднеквадратическое отклонение:
4) Размах выборки: 5) Начальные моменты: – 1-го порядка – 2-го порядка – 3-го порядка
– 4-го порядка
6) Центральные моменты – 2-го порядка – 3-го порядка
– 4-го порядка
7) Асимметрия
8) Эксцесс Так как
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 242. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
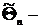 точечная оценка для параметра
точечная оценка для параметра 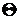 генеральной совокупности.
генеральной совокупности.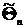 называется несмещённой, если её математическое ожидание равно оцениваемому параметру, т.е.
называется несмещённой, если её математическое ожидание равно оцениваемому параметру, т.е. 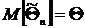 .
.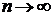 стремится по вероятности к оцениваемому параметру
стремится по вероятности к оцениваемому параметру 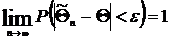 .
.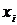
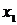
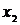
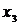
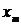
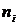
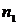
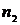
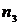
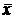 ) – это среднее арифметическое всех значений выборки:
) – это среднее арифметическое всех значений выборки: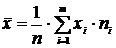 или
или 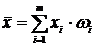 .
.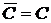 , где С – постоянная;
, где С – постоянная;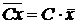 ;
;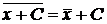 ;
;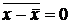 ;
;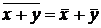 .
.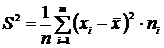 .
.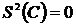 , где С – постоянная;
, где С – постоянная;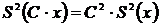 ;
;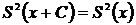 ;
;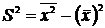 , где
, где 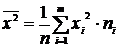
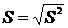 .
.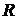 ) – это разность между максимальной и минимальной вариантами или длина интервала, которому принадлежат все варианты выборки:
) – это разность между максимальной и минимальной вариантами или длина интервала, которому принадлежат все варианты выборки: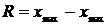 .
.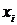 от некоторой постоянной величины
от некоторой постоянной величины 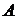 называется моментом k-го порядка:
называется моментом k-го порядка: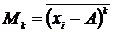 .
.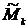 ), а при использовании вероятностей – теоретическими (обозначаются
), а при использовании вероятностей – теоретическими (обозначаются 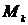 ). Порядок момента определяется величиной k.
). Порядок момента определяется величиной k.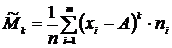 .
.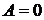 , то моменты начальные;
, то моменты начальные; 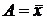 , то моменты центральные;
, то моменты центральные; 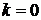
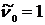
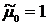
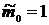
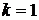
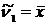
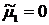
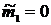
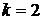
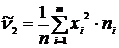
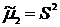
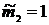

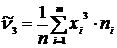
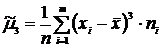
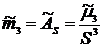
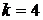
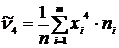
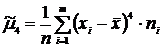
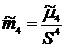
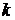
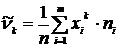
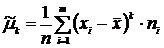
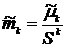
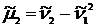 ,
,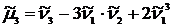 ,
,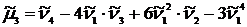 .
.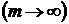 и одновременного уменьшении интервала группировки полигон либо гистограмма распределения всё более и более приближается к некоторой плавной кривой, являющейся для указанных графиков пределом. Эта кривая называется эмпирической кривой распределения и представляет собой графическое изображение в виде непрерывной линии изменения частот, функционально связанного с изменением вариант. В статистике различают следующие виды кривых распределения: одновершинные и многовершинные кривые.
и одновременного уменьшении интервала группировки полигон либо гистограмма распределения всё более и более приближается к некоторой плавной кривой, являющейся для указанных графиков пределом. Эта кривая называется эмпирической кривой распределения и представляет собой графическое изображение в виде непрерывной линии изменения частот, функционально связанного с изменением вариант. В статистике различают следующие виды кривых распределения: одновершинные и многовершинные кривые.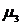 . Чтобы получить безразмерную характеристику, его делят на
. Чтобы получить безразмерную характеристику, его делят на 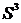 (так как
(так как 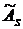 – это отношение центрального момента третьего порядка к кубу выборочного среднеквадратического отклонения:
– это отношение центрального момента третьего порядка к кубу выборочного среднеквадратического отклонения: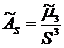 .
.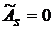 . Если
. Если 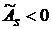 , то имеет место левосторонняя асимметрия, а если
, то имеет место левосторонняя асимметрия, а если  – правосторонняя асимметрия. Чем ближе по модулю
– правосторонняя асимметрия. Чем ближе по модулю 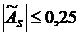 , то асимметрия считается незначительной,
, то асимметрия считается незначительной,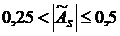 , то асимметрия считается умеренной,
, то асимметрия считается умеренной,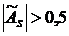 , то асимметрия значительная.
, то асимметрия значительная.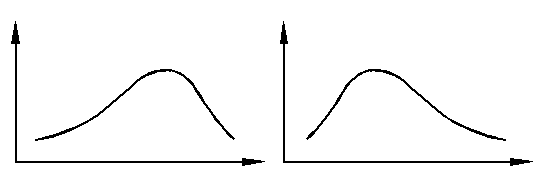
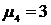 , поэтому для оценки крутизны исследуемого распределения в сравнении с нормальным из
, поэтому для оценки крутизны исследуемого распределения в сравнении с нормальным из 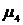 вычитается 3. Эксцесс
вычитается 3. Эксцесс 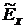 – это уменьшённое на три единицы отношение центрального момента четвёртого порядка к четвёртой степени среднеквадратического отклонения:
– это уменьшённое на три единицы отношение центрального момента четвёртого порядка к четвёртой степени среднеквадратического отклонения: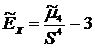 .
.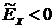 , менее крутые, имеют более плоскую вершину и называются плосковершинными. Кривые распределения, у которых
, менее крутые, имеют более плоскую вершину и называются плосковершинными. Кривые распределения, у которых 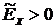 , более крутые, имеют острую вершину и называются островершинными.
, более крутые, имеют острую вершину и называются островершинными.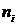
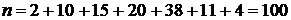 .
.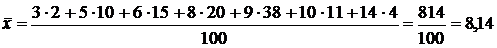 .
.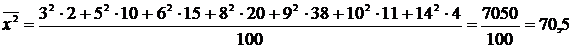 ;
;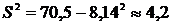 .
.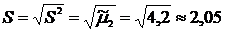 .
.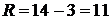 .
.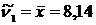 ;
;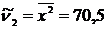 ;
;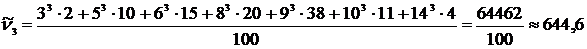 ;
;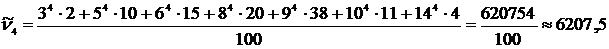 .
.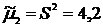 ;
;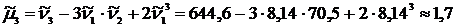 ;
;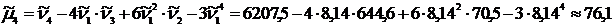 .
.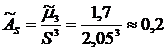 .
.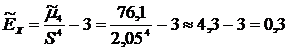 .
.