
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Энергия, потребляемая индуктивностью, работы не совершает.Мкость (С)
Рис.2.7. Условно положительные направления тока
Пусть через емкость протекает синусоидальный ток i= Imsinwt. По определению Для емкости: q = CU. (2.16) Для линейного конденсатора C = const, поэтому i = откуда где XC = Ток в ёмкости опережает приложенное напряжение на угол 900, также можно считать, что напряжение отстаёт от тока на 900. Определим мгновенную мощность: p = ui = UIsin2wt. (2.18) Среднее значение мощности за период:
Таким образом, идеальная емкость не потребляет из сети мощность.
Для оценки запасенной в емкости энергии электрического поля вводят понятие реактивной мощности, равной:
График функции мгновенной мощности представлен на рис.2.8. Здесь, где p > 0, энергия идёт на создание электрического поля, где p < 0, происходит возврат энергии.
Рис.2.8. Графики мгновенных значений тока, напряжения и мощности на емкости
Изображение синусоидальных функций (напряжение, сила тока, мощность) векторами на комплексной плоскости Расчет сложной разветвленной цепи может быть существенно упрощен, если заменить синусоидальные токи и напряжения векторами, расположенными на комплексной плоскости. Такой метод получил название метода комплексных амплитуд. В основе данного метода лежит формула Эйлера:
где j = Умножив обе части на А, получим: A где A = 
Рис.2.9. Изображение вектора (w - угловая частота вращения вектора Поскольку в формуле Эйлера a может быть любым, мы сделаем его линейной функцией времени: a = wt + y. (2.22) Тогда: Полученный результат (2.24) показывает, что синусоидальная функция времени есть мнимая часть некоторого комплексного числа: а = Asin(wt +y) = ImAej(wt+y); (2.24) при условии, что t = 0 получим:
Векторная диаграмма - диаграмма векторов на комплексной плоскости, построенная с учетом их взаимной ориентации по фазе. Если вектора вращаются на плоскости с одинаковыми частотами w, то их взаимное положение не меняется, это свойство позволяет исключить из рассмотрения сам факт их вращения, то есть принимать t = 0. В качестве примера на рис.2.10 изображена операция умножения некоторого вектора Пусть модуль
По формуле Эйлера:
Рис.2.10. Умножение вектора на +j и –j Основы символического расчета цепей синусоидального тока Этот метод позволяет перейти от дифференциальных уравнений, составленных для мгновенных токов, напряжений и т.д., к алгебраическим уравнениям, составленным для соответствующих им комплексных изображений.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 527. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 , где q – заряд.
, где q – заряд. , (2.17)
, (2.17)

 – емкостное (реактивное) сопротивление.
– емкостное (реактивное) сопротивление. . (2.19)
. (2.19) , [вар]. (2.20)
, [вар]. (2.20)
 , (2.21)
, (2.21) .
. = A1+A2,
= A1+A2,  - модуль комплексного числа;
- модуль комплексного числа;  - аргумент комплексного числа.
- аргумент комплексного числа.
 на комплексной плоскости
на комплексной плоскости )
) . (2.23)
. (2.23) Þ
Þ  = A
= A  (2.25)
(2.25) на оператор поворота j.
на оператор поворота j. = 10А. Его положение на комплексной плоскости зависит от значения аргумента. Значениям y = 0, 900, - 900 соответствуют комплексные числа
= 10А. Его положение на комплексной плоскости зависит от значения аргумента. Значениям y = 0, 900, - 900 соответствуют комплексные числа  :
: ;
;  ;
;  .
. ;
;  ;
;  ;
; 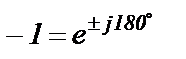 .
.