
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКАРассмотренные выше источники энергии могут быть как постоянными, так и переменными, причем закон их изменения во времени может носить как периодический, так и непериодический характер. Наибольшее практическое распространение получили источники, а следовательно и цепи, электромагнитные процессы в которых подчиняются периодическому закону. Частным случаем таких цепей являются цепи однофазного синусоидального тока. Мгновенное значение любой синусоидальной функции: напряжения, тока, ЭДС и т.д. может быть представлено выражением вида: u(t) = Um sin(wt+y), (2.1) где Um – амплитуда – наибольшее значение функции за период Т (рис.2.1); w – круговая (циклическая) частота колебания; y – начальная фаза, которая показывает смещение синусоиды относительно начала координат вправо или влево; T = 1/¦ Þ ¦ = 1/T, [Гц]; (2.2) w = 2p¦ = 2p/Т, [рад/с]. (2.3)
Рис.2.1. Примеры изображения периодических функций Среднее и действующее значение периодической функции Fср= где f(t) – периодическая функция, T – период периодической функции. Ввиду симметричности синусоиды получаем, что среднее значение за период равно нулю, поэтому вводят понятие среднего значения за половину периода.
 = = 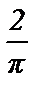 Fm; Fm;
Fср = Значительно большее значение имеет понятие действующего значения. Для его осмысления оценим тепловое действие переменного и постоянного тока. Переменный ток: W = Постоянный ток: W = I2RT; Приравняв правые части и произведя простые операции, получим:  I = IД = где Подставим полученный результат под корень и получим: I = где (2.7) – среднеквадратичное, эффективное или действующее значение синусоидального тока. Аналогично,
Рис.2.2. Графическое изображение действующего значения
Элементы R,L,C в цепях синусоидального тока
2.2.1. Сопротивление (R) Пусть по сопротивлению протекает синусоидальный ток с начальной фазой равной нулю. i = Imsinwt. (2.8)
Рис.2.3. Условно положительные направления тока
Определим падение напряжения, действующее на зажимах сопротивления на основании закона Ома: u = iR = ImRsinwt = Umsinwt. (2.9) Полученный результат показывает, что напряжение изменяется в фазе с током. Определим функцию мгновенной мощности, потребляемую R.
p = UI(1 – cos2wt), (2.10) где U, I – действующие значения.
Рис.2.4. Графики мгновенных значений напряжения, тока
Из графика мгновенной мощности следует, что она неотрицательна и меняется с удвоенной частотой. Для оценки потребляемой приемником мощности вводят понятие средней мощности за период:
Индуктивность (L) Пусть через индуктивность протекает синусоидальный ток: i = Imsinwt;
Рис.2.5. Условно положительные направления тока, напряжения и ЭДС самоиндукции
Определим падение напряжения на индуктивности uL. На основании закона электромагнитной индукции: eL = – L где uL = -eL = Umsin(wt + p/2). (2.12) Напряжение на индуктивности опережает ток на 900. Мгновенная мощность на индуктивности: p = ui = (UmImsin2wt)/2=UIsin2wt. (2.13) Среднее значение мощности за период:
Для оценки занесенной в индуктивности энергии магнитного поля вводят понятие реактивной (индуктивной) мощности:
Рис.2.6. Графики мгновенных значений напряжения, тока и мощности на индуктивности
Из графика мгновенной мощности следует, что положительная полуволна мощности соответствует потреблению энергии из сети, а отрицательная – ее возврату в сеть. |
|||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 426. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 , (2.4)
, (2.4) =
=  Fm. (2.5)
Fm. (2.5) ;
; , (2.6)
, (2.6)
 =
=  ;
; , (2.7)
, (2.7) .
.

 ;
;
 , [Вт]. (2.11)
, [Вт]. (2.11)
 = – wLImcoswt = wLImsin(wt–p/2) = XLImsin(wt–p/2),
= – wLImcoswt = wLImsin(wt–p/2) = XLImsin(wt–p/2), – индуктивное (реактивное) сопротивление.
– индуктивное (реактивное) сопротивление. . (2.14)
. (2.14) ,[вар] (2.15)
,[вар] (2.15)