
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства неопределенного интеграла ⇐ ПредыдущаяСтр 8 из 8 1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению:
2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т.е.
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
4. Неопределенный интеграл от алгебраической суммы функций равен такой же алгебраической сумме неопределенных интегралов от каждой функции:
Основные формулы интегрирования (табличные интегралы). Из каждой формулы дифференцирования вытекает соответствующая ей формула интегрирования. Например, из того, что Ниже приведена таблица основных табличных интегралов: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Справедливость этих формул можно проверить дифференцированием. Непосредственное интегрирование. Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам. Пример 1.Найти интеграл Решение. Воспользуемся определением степени с отрицательным показателем (
Пример 2.Найти интеграл Решение. Воспользуемся определением степени с дробным показателем (
Пример 3.Найти интеграл Решение. Воспользуемся определением степени с дробным показателем и правилом умножения степеней с одинаковыми основаниями ( 
Пример 4.Найти интеграл Решение. Воспользуемся определением степени с дробным показателем (
Пример 5.Найти интеграл Решение. Раскроем скобки по формуле
Пример 6.Найти интеграл Решение. Для нахождения интеграла воспользуемся формулой
Интегрирование методом подстановки. Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки. Сущность метода заключается в том, что путем введения новой переменной удается свести данный интеграл к новому интегралу, который сравнительно легко берется непосредственно. Для интегрирования методом подстановки можно использовать следующую схему: 1) часть подынтегральной функции надо заменить новой переменной; 2) найти дифференциал от обеих частей замены; 3) все подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл); 4) найти полученный табличный интеграл; 5) сделать обратную замену. Пример 7.Найти интеграл Решение. Произведем подстановку
Пример 8.Найти интеграл Решение. Сначала положим
Пример 9.Найти интеграл Решение. Положим
Пример 10.Найти интеграл Решение. Положим
В практике интегрирования часто встречаются интегралы, для нахождения которых можно использовать следующие формулы ( 1. 2. 3. 4. 5. 6. 7. 8. Так, при нахождении Интегрирование по частям.Здесь используют формулу: Пример 11. Найти интеграл:
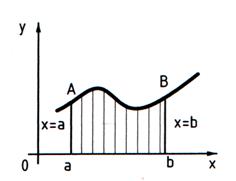
Определенный интеграл. Понятие определенного интеграла. Пусть функция
где Геометрически (рис. 10) каждое слагаемое интегральной суммы равно площади прямоугольника с основанием
Рисунок 10
Очевидно, что при всевозможных разбиениях отрезка Будем увеличивать число точек разбиения так, чтобы длина наибольшего из отрезков Этот предел и называется определенным интегралом от функции Определение 4. Определенным интегралом от функции По определению,
Число a называется нижним пределом интегрирования, число b – верхним; отрезок Заметим, что всякая непрерывная на отрезке Если интегрируемая на отрезке Основные свойства определенного интеграла. Все свойства сформулированы в предположении, что рассматриваемые функции интегрируемы в соответствующих промежутках. 1. Определенный интеграл с одинаковыми пределами равен нулю:
2. При перестановке пределов интегрирования знак интеграла меняется на противоположный:
3. Отрезок интегрировании можно разбивать на части:
4. Постоянный множитель можно выносить за знак интеграла:
5. Интеграл от алгебраической суммы функций равен такой же алгебраической сумме интегралов от всех слагаемых:
Непосредственное вычисление определенного интеграла. Для вычисления определенного интеграла, когда можно найти соответствующий интеграл, служит формула Ньютона-Лейбница
Т.е. определенный интеграл равен разности значений любой первообразной функции при верхнем и нижнем пределах интегрирования. Из этой формулы виден порядок вычисления определенного интеграла: 1) найти неопределенный интеграл от данной функции; 2) в полученную первообразную подставить вместо аргумента сначала верхний, затем нижний предел интеграла; 3) из результата подстановки верхнего предела вычесть результат подстановки нижнего предела. Пример 14.Вычислить интеграл Решение. Применив указанное правило, вычислим данный определенный интеграл:
Пример 15.Вычислить интеграл Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:
Пример 16.Вычислить интеграл Решение. Интеграл от разности функций заменим разностью интегралов от каждой функции:
Пример 17.Вычислить интеграл Решение. Воспользуемся определением степени с дробным показателем, правилом деления суммы на число и вычислим определенный интеграл от каждого слагаемого отдельно:
Вычисление определенного интеграла методом подстановки. Вычисление определенного интеграла методом подстановки состоит в следующем: 1) часть подынтегральной функции заменить новой переменной; 2) найти новые пределы определенного интеграла; 3) найти дифференциал от обеих частей замены; 4) все подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл); 5) вычислить полученный определенный интеграл. Пример 18.Вычислить интеграл Решение. Введем подстановку Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
Пример 19.Вычислить интеграл Решение. Произведем подстановку Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
Пример 20.Вычислить интеграл Решение. Положим Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
Пример 21.Вычислить интеграл Решение. Пусть
Пример 22.Вычислить интеграл Решение. Сначала преобразуем подынтегральное выражение:
Затем вычислим интеграл от разности функций, заменив его разностью определенных интегралов от каждой функции:
Вычислим каждый интеграл отдельно:
Пусть
Тогда
Интегрирование по частям.Здесь используют формулу: Пример 23.Вычислите интеграл: Пример 24.Вычислите интеграл: Приложение определенного интеграла. Понятие определенного интеграла широко применяется для вычисления различных геометрических и физических величин. Площади плоских фигур. 1. Фигура ограниченная графиком непрерывной и неотрицательной на отрезке [a;b] функции f(x), осью Ох и прямыми х = а, х = b. Площадь данной фигуры находится по S =
Пример 25: Вычислить площадь фигуры ограниченной линиями
Находим доп. точки, для этого строим таблицу:
в) х = - 2, х = 3 – прямые, У у =
- 2 1 3
S = Пример 26: Вычислить площадь фигуры ограниченной линиями y = - x2 – 1, y = 0, x = - 1, x = 2. Решение: Построим графики данных функций: а) у = - х2 – 1 – квадратичная функция, графиком является парабола, ветви направлены вниз. Вершина находится в точке с координатами (0; - 1). Находим доп. точки, для этого строим таблицу:
б) у = 0 – ось Ох; х = - 1, х = 2 – прямые параллельные оси Оу
Х = -1 Х = 2
У = - х2 – 1
I = S = 2. Фигура, ограниченная графиками двух непрерывных на отрезке [a; b] функций f(x) и g(x) и прямыми x = a, x = b, где f(x) ≥ g(x). В этом случае искомая площадь вычисляется по формуле S =
Пример 27: Вычислить площадь фигуры ограниченной линиями Решение:1) Найдем пределы интегрирования, т.е. абсциссы точек пересечения графиков функций
Имеем
D = D = (- 1)2 - 4· 1· ( - 2) =9 Следовательно a = - 1, b = 2 2)Построим графики функций: а) y = 4 – x2 - квадратичная функция, график – парабола, ветви вниз. Вершина находится в точке с координатами (0;4). Находим доп. точки, для этого строим таблицу:
б) y = x2 - 2x – квадратичная функция, график – парабола, ветви направлены вверх. Найдем координаты вершины параболы: хв = - Вершина находится в точке с координатами (1; - 1). Находим доп. точки, для этого строим таблицу:
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 239. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  .
.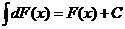 .
. .
. .
. , следует равенство
, следует равенство  .
.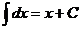



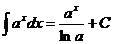

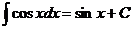




 .
.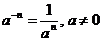 ) и найдем неопределенный интеграл от степени:
) и найдем неопределенный интеграл от степени: .
. .
. ) и найдем неопределенный интеграл от степени:
) и найдем неопределенный интеграл от степени: .
. .
. ) и найдем неопределенный интеграл от степени:
) и найдем неопределенный интеграл от степени: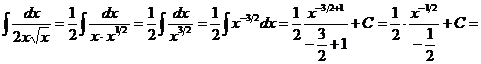

 .
. ), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеем
), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеем

 .
. и неопределенный интеграл от полученной алгебраической суммы функций заменим такой же алгебраической суммой неопределенных интегралов от каждой функции:
и неопределенный интеграл от полученной алгебраической суммы функций заменим такой же алгебраической суммой неопределенных интегралов от каждой функции: .
. .
. и свойствами неопределенного интеграла:
и свойствами неопределенного интеграла: .
. .
.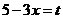 , тогда
, тогда  , откуда
, откуда 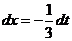 . Далее получаем
. Далее получаем .
. .
. , тогда
, тогда  , откуда
, откуда  . Далее получаем
. Далее получаем
 .
. , тогда
, тогда  откуда
откуда  . Далее получаем
. Далее получаем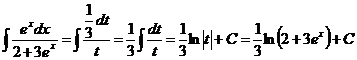 .
. .
. , тогда
, тогда  , откуда
, откуда  . Далее получаем
. Далее получаем .
.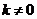 ,
,  - постоянные):
- постоянные):


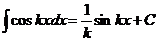




 , где
, где  . Тогда
. Тогда  .
.
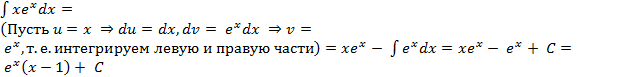 Пример 12. Найдите интеграл:
Пример 12. Найдите интеграл:  Пример 13. Найдите интеграл:
Пример 13. Найдите интеграл: 
 определена на отрезке
определена на отрезке  . Допустим для простоты, что функция
. Допустим для простоты, что функция 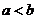 . Разобьем этот отрезок на n частей точками
. Разобьем этот отрезок на n частей точками  . На каждом из частичных отрезков
. На каждом из частичных отрезков  (i=1, 2, 3, …, n) возьмем произвольную точку
(i=1, 2, 3, …, n) возьмем произвольную точку  и составим сумму:
и составим сумму: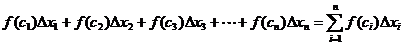 ,
, . Эта сумма носит название интегральной суммы функции
. Эта сумма носит название интегральной суммы функции  и высотой
и высотой  , а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.
, а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.
 на части получим различные интегральные суммы, а, следовательно, и различные «ступенчатые фигуры».
на части получим различные интегральные суммы, а, следовательно, и различные «ступенчатые фигуры». , ни от того, как выбираются точки
, ни от того, как выбираются точки  и читается «интеграл от a и b от функции
и читается «интеграл от a и b от функции  » или, короче, «интеграл от a и b от функции
» или, короче, «интеграл от a и b от функции  .
. , осью абсцисс и прямыми
, осью абсцисс и прямыми  и
и  (рис. 10), т.е.
(рис. 10), т.е.  . В этом и заключается геометрический смысл определенного интеграла.
. В этом и заключается геометрический смысл определенного интеграла.
 .
.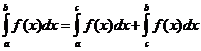 , где
, где 

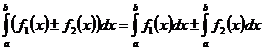
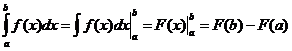 ,
,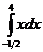 .
.
 .
.
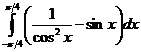 .
.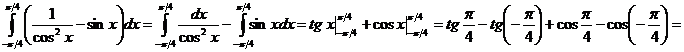
 .
. .
.
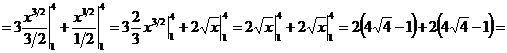

 .
. , тогда
, тогда  ,
,  . Определим пределы интегрирования для переменной t. При x=0 получаем
. Определим пределы интегрирования для переменной t. При x=0 получаем  , при x=7 получаем
, при x=7 получаем  .
. .
. .
. , тогда
, тогда  ,
,  . Определим пределы интегрирования для переменной t. При x=1 получаем
. Определим пределы интегрирования для переменной t. При x=1 получаем  , при x=2 получаем
, при x=2 получаем 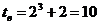 .
. .
. .
. , тогда
, тогда  ,
, 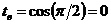 .
.

 .
. ,
,  ,
,  ,
,  .
.
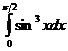 .
.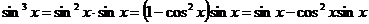 .
. .
. ;
; ,
,  .
. .
.


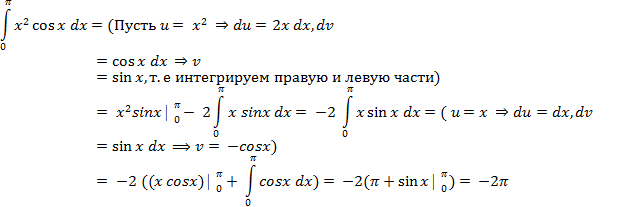
 (1)
(1)
 . Решение: Построим графики данных функций: а)
. Решение: Построим графики данных функций: а)  - кв. ф., график – парабола, ветви направленны вверх. Вершина находится в точке с координатами (0; 1).
- кв. ф., график – парабола, ветви направленны вверх. Вершина находится в точке с координатами (0; 1).

 5,5
5,5
 б) у = 0 – ось Ох
б) у = 0 – ось Ох
 параллельные оси Оу
параллельные оси Оу


















 У
У


 0 Х
0 Х














 - 2 - 1 1 2 3
- 2 - 1 1 2 3

 (2)
(2)

 ,
,  .
.

 ,
, 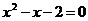 , a = 1, b= - 1, c = - 2
, a = 1, b= - 1, c = - 2
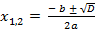
 ,
,  ,
,  .
. .
.
 У
У
 0
0
 у = х2 – 2х
у = х2 – 2х