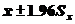Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫЗадача 1. Время (в минутах) обслуживания клиентов в железнодорожной кассе представлено выборкой: 2,0; 1,5; 1,0; 1,0; 1,25; 3,5; 3,0; 3,0; 3.75; 3,7; 4,0; 6,0; 7,0; 1,5; 8,0; 3,5; 5,0; 3,5; 14,0; 12,0; 15,1; 18,0; 18,5; 17,0. Определите процент клиентов, время обслуживания которых более 12 минут и менее 5 минут. Задача 2. Из генеральной совокупности извлечена выборка объема n=16:
Оцените с надежностью 0,9 математическое ожидание α нормально распределенного признака генеральной совокупности с помощью доверительного интервала. Задача 3 . Результаты исследования длительности оборота оборотных средств торговых фирм города (в днях) представлены в группированном виде:
Постройте доверительный интервал с надежностью 0,95 для средней длительности оборотных средств торговых фирм города при условии, что среднее квадратическое отклонение
Реализация описательной статистики и частотного анализа в программе SPSS К группе описательных статистических характеристик относятся: 1. Меры средней тенденции:среднее арифметическое, медиана, квантили (квартили, децили, процентили), сумма, мода 2. Меры разброса:размах вариации, стандартное (среднее квадратическое отклонение) Стандартная ошибка среднего S.E. – мера того, насколько значение среднего может варьироваться от выборки к выборке из одного распределения, Стандартная ошибка среднегоможет использоваться для грубого сравнения наблюдаемого значения среднего и гипотетического (две переменные различны, если соотношение S.E. меньше «минус 2» или больше «плюс 2»).  Стандартную ошибку можно использовать для оценки доверительного интервала среднего. Доверительный интервал (истинное значение среднего параметра) – это интервал со случайными границами, накрывающий значение параметра с заданной (доверительной) вероятностью. В частности, приближенными оценками границ 95% двустороннего доверительного интервала являются значения с вероятностью 0.95 находится в этих пределах); Дисперсия – мера рассеяния, сумма квадратов отклонения значений от среднего, деленная на число случаев минус 1. Меры несимметричности распределений Для отражения близости формы распределения к нормальному виду существуют две основные характеристики. Эксцесс является мерой «сглаженности» (островершинности или плосковершинности) распределения. Если значение эксцесса близко к 0, это означает, что форма распределения близка к нормальному виду. Положительный эксцесс указывает на «плосковершинное» распределение, у которого максимум вероятности выражен не столь ярко, как у нормального. Значения эксцесса, превышающие 5,0, говорят о том, что по краям распределения находится больше значений, чем вокруг среднего. Отрицательный эксцесс, напротив, характеризует «островершинное» распределение, график которого более вытянут по вертикальной оси, чем график нормального распределения. Считается, что распределение с эксцессом в диапазоне от –1 до +1 примерно соответствует нормальному виду. В большинстве случаев вполне допустимо считать нормальным распределение с эксцессом, по модулю не превосходящим 2. Коэффициент вариации (эксцесс) – мера степени сгруппированности значений вокруг среднего Коэффициент вариации указывает, является ли форма распределения значений признака пологим (при большом значении коэффициента) или крутым. |
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 530. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
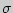 неизвестно (известно и равно 10 дням).
неизвестно (известно и равно 10 дням).