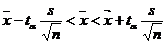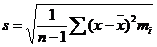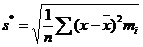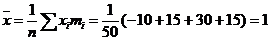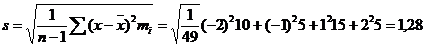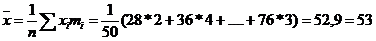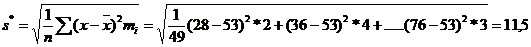Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
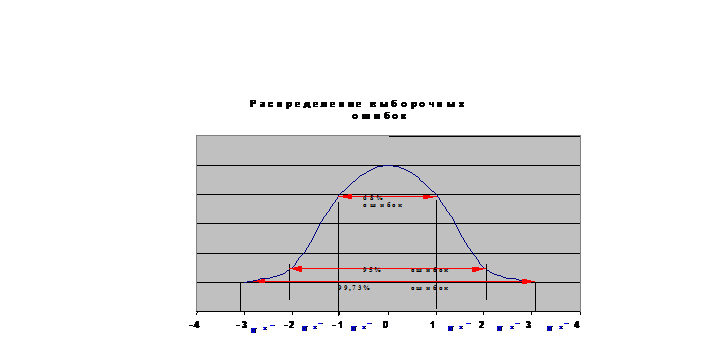
Дисперсия распределения ошибок равна дисперсии распределения выборочных средних.В контексте программы SPSS стандартная ошибка используется для среднего значения, асимметрии и эксцесса Стандартная ошибка (standard error) является характеристикой точности, или стабильности, величины, для которой она вычисляется. Ее смысл заключается в следующем. Можно взять некоторое количество случайно выбранных значений генеральной совокупности, составить выборку и вычислить для нее среднее значение. Повторив эту операцию несколько раз, вы получите набор средних значений выборок, которые также представляют собой некоторое распределение. Стандартное отклонение этого распределения и будет являться стандартной ошибкой для среднего значения генеральной совокупности. Аналогичным способом вычисляются стандартные ошибки для асимметрии и эксцесса. Чем меньше значение стандартной ошибки, тем выше стабильность величины, для которой она вычисляется. Форма распределения ошибок выборок такая же, как у распределения выборочных средних, то есть оба распределения можно считать нормальными или похожими на них.
Для любого нормального распределения 95% наблюдений попадают в интервал ±2 стандартных отклонения от среднего, 68 наблюдений % – в интервал ±1,99. Так как среднее генеральной совокупности μ = а ошибка среднего – это стандартное отклонение ошибок выборок, то можно заключить, что с 95% вероятностью доверительный интервал для среднего генеральной совокупности μ. μ = При этом распределение выборочных средних должно быть нормальным, что имеет место либо когда распределение выборочной совокупности является нормальным, либо когда в выборке число наблюдений составляет величину более 30.  Чтобы посчитать ошибку среднего, нам надо знать число выборки и стандартное отклонение генеральной совокупности, которое как правило, неизвестно. Доказано, что соотношение между генеральной дисперсией σ² и выборочной дисперсией S2 определяется следующим равенством: σ² = S²(n/(n–1)). Если n велико, то сомножитель n/(n – 1) ≈ 1 и можно принять выборочную дисперсию в качестве оценки величины генеральной дисперсии. Поэтому стандартное отклонение выборки S можно принимать как приближенное значение стандартного отклонения генеральной совокупности σ. Тогда вместо формулы
можно использовать
или с 95% вероятностью: μ = Зачастую в исследованиях используется уровень доверия 90, 95 или 99 %. В зависимости от выбранного доверительного уровня определяется константа доверительных уровней z, участвующая в формуле расчета статистической ошибки выборки. Константы доверительных уровней
Максимальная статистическая ошибка выборки рассчитывается по следующей формуле:
p=q=50% – вероятность наступления/ненаступления исследуемого события (то есть попадания/непопадания респондента в выборку); для случайных выборок данная вероятность равна 1/2 или 50 %; n — размер выборки (общее количество опрошенных). Таким образом, для выборки в 1000 респондентов и при уровне доверия к результатам опроса 95 % статистическая ошибка выборки будет равна:
Доверительным называется интервал, который с заданной надежностью α покрывает оцениваемый параметр. Доверительный интервал служит для оценки математического ожидания α случайной величины X, распределенной по нормальному закону, при известном среднем квадратическом отклонении Ϭ
Пример: найти доверительный интервал для оценки с надежностью 0,9 неизвестного математического ожидания α нормально распределенного признака X генеральной совокупности, если среднее квадратическое отклонение Ϭ=5, выборочная средняя Решение. Требуется найти доверительный интервал Найдем t из соотношения Ф(t)= 0,9/2= 0,45 =0,6 . По таблице приложения функции Лапласа находим t=0,6 получаем доверительный интервал Если среднее квадратическое отклонение неизвестно, то для оценки величины точности оценки служит доверительный интервал
где tα находится в таблицах по заданным n и α, а вместо s часто бывает возможно подставить любую из оценок
- исправленное среднеквадратическое, статистическое среднеквадратическое отклонения соответственно. При увеличении n обе оценки будут различаться сколь угодно мало и будут сходиться по вероятностям к одной и той же величине Ϭ. Пример 167.Из генеральной совокупности извлечена выборка объема n = 50:
Оценить с надежностью 0,95 математическое ожидание α нормально распределенного признака генеральной совокупности по выборочной средней. Решение. Выборочную среднюю и исправленное среднее квадратическое отклонение найдем соответственно по формулам
Для α=0,95 и n =50 t=2,01 доверительный интервал: 0,64<x<1,36 Пример:Результаты исследования длительности оборота (в днях) оборотных средств торговых фирм города представлены в группированном виде:
Построить доверительный интервал с надежностью 0,99 для средней длительности оборотных средств торговых фирм города. Решение. Найдем выборочную среднюю длительности оборотных средств.
Для α=0,99 и n =50 t=2,68 доверительный интервал: 48,6<x<57,3 |
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 557. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
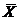 ± ошибка среднего
± ошибка среднего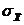
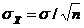
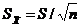
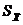

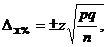
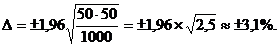
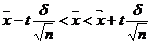
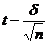 – точность оценки
– точность оценки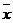 – выборочное среднее
– выборочное среднее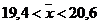 .
.