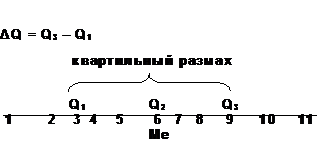Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Меры средней тенденции и разброса вариаций значений признака.Признак– некоторое общее для всех изучаемых объектов качество, конкретные проявления которого меняются от объекта к объекту и могут быть измерены. Значение признака – конкретное проявление того или иного признака. В анализе данных важное значение имеет построение частотных таблиц, предназначенных для описания данных, их компактного представления и формулировки предварительных выводов относительно исследуемых вопросов.
Меры центральной тенденции указывают на расположение среднего, или типичного, значения признака, вокруг которого предположительно сгруппированы остальные наблюдения. Мода – это такое значение признака, которое встречается чаще всего. Мода рассчитывается для любого типа шкал. Например, в представленном ниже числовом ряде модальным будет являться значение 3. 3, 4, 5, 3, 3, 3, 4, 4, 5, 3, 3 Числовой ряд может содержать не обязательно одну, но и две, и три моды. Например, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4 содержит две моды «1» и «2». Медиана – это значение признака, которое делит ранжированный вариационный ряд на две равные части, так что 50% наблюдений оказывается меньше медианы, а 50% наблюдений – больше медианы.  Медиана – это 3-й квартиль распределения. Например: 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3. Медианное значение равняется 2. Если число переменных в группе наблюдений четное, то медианой будет среднее двух центральных значений. Среднее арифметическое отношениесумы всех значений наблюдений к общему числу наблюдений:
где Хi – наблюдаемые значения, n – число наблюдений. Суть данной меры в том, что сумма расстояний от среднего арифметического до объектов, имеющих большее значение, равна сумме расстояний до объектов, имеющих меньшее значение. Поэтому, естественно, что мы можем ее использовать только для шкал, где вычисление расстояний между объектами имеет смысл, то есть для числовых шкал. Для номинальных дихотомических признаков, закодированных нулями и единицами, можно считать среднее арифметическое (и соответственно дисперсию), нужно лишь уметь правильно интерпретировать полученный результат. Например: 0 – мужчины; 1 – женщины. Тогда среднее значение будет равно k/n, где k – число женщин (или признаков равных 1). Если `Х = 0, значит в нашей выборке одни мужчины. Если `Х = 1, значит в нашей выборке одни женщины. Если `Х = 0,5, значит половина женщин и половина мужчин. Если 0 <`Х < 0,5 – в совокупности женщин меньше 50%. Если 0,5 <`Х < 0 – в совокупности женщин больше 50%. При работе с мерами центральной тенденции следует учитывать, что для каждого типа шкал следует вычислять различные меры центральной тенденции.
Следует учитывать, что меры центральной тенденции адекватно отражают реальную ситуацию только для однородной совокупности, а выбор и расчет таких мер определяется общей формой распределения. Важной мерой вариации является понятие квартиля. Первый квартиль отсекает 25% наблюдений с наименьшим значением признака, второй (медиана) – 50% наблюдений, третий квартиль – 75% наблюдений. Квартильный размах – интервал, в котором вокруг медианы сосредоточилось 50% респондентов. Квартильный размах является единственной мерой вариации для порядковых шкал.
Дисперсия позволяет судить об отклонениях каждого отдельного наблюдаемого значения от среднего. Чем меньше значение дисперсии, тем более однородной является совокупность. Для дихотомических признаков дисперсию можно интерпретировать следующим образом: дисперсия равна нулю, если все объекты либо обладают, либо не обладают анализируемым свойством, т.е. если совокупность однородна, а ее максимальное значение достигается в случае равномерного распределения. Стандартное отклонение – величина, равная квадратному корню из дисперсии. Для любого нормального распределения, не менее 68% наблюдений будут попадать в промежуток ± одно стандартное отклонение от среднего арифметического значения, для ± трех стандартных отклонений внутри указанного интервала окажутся не менее 99,97% наблюдений.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 551. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
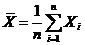 ,
,