Основные понятия и определения

Пусть Х – некоторое счетное множество точек (х₁, х₂, …, x_n) пространства Rⁿ.

Функцией нескольких переменных (n переменных) называется соответствие (закон) f, согласно которому каждой точке множества Х сопоставляется определенное число z. Такое соответствие записывается в виде z = f (x₁, x₂, …, x_n). При этом множество Х назы­­вается областью определения функции f.

Для наглядности и простоты изложения в рамках этой темы мы ограничимся рассмотрением функций двух переменных (n = 2), хотя все основные понятия достаточно легко обобщаются на случай любого конечного числа переменных.

Функцию двух переменных z = f (x, y) можно изобразить графи­чески, вычисляя для каждой точки (x, y) области ее определения Х значение функции z. В этом случае мы получим некоторую совокуп­ность точек трехмерного пространства (x, y, z), которая и будет являться графиком функции. В самом общем случае график функции двух переменных представляет собой некоторую поверхность в трехмерном пространстве. Например, на рис. 19 приведен график функции двух переменных z = x² + y².

Рис. 19.

ПРИМЕРЫ:

1. Многомерная функция полезности z = f (x₁, x₂, …, x_n) есть числовая оценка определенным индивидом полезности набора приобретенных им n товаров.

2. Производственная функция Кобба-Дугласа: , где А, α и β – неотрицательные константы, х₁ – объем производ­ствен­ных фондов, х₂ – объем трудовых ресурсов, z – объем выпуска продукции.

График функции двух переменных представляет собой значительно более сложный объект, чем график функции одной переменной. Чаще всего, графическое представление на плоскости достаточно сложной поверхности – графика функции встречает серьезные трудности, а самое главное, не обладает достаточной информативностью. Поэтому для изучения свойств функций двух переменных вместо графика используют так называемые линии уровня.

Линией уровня функции двух переменных z = f (x, y) называется множество точек плоскости Oxy таких, что во всех этих точках значение функции равно постоянной величине С, Число С в этом случае называется уровнем.

Фактически линии уровня представляют собой «срезы» (сечения) поверхности графика функции плоскостями с уравнениями f (x, y) = C, параллельными плоскости Oxy. Для примера на рис. 20 приведены линии уровня для некоторой функции двух переменных.

Рис. 20.

Предел и непрерывность

Для дальнейшего нам понадобится понятие δ – окрестности точ­ки на плоскости Oxy.

Для любого числа δ > 0 δ – окрестностью точки (x₀, y₀) называется множество всех точек плоскости (x, y), для которых выполняются неравенства  и .

Число А называется пределом функции z = f (x, y) при x→x₀ и y→y₀ (или в точке M₀(x₀, y₀)), если для любого числа ε > 0 найдется число δ > 0 такое, что для всех точек M(x, y), лежащих в δ – окрест­ности точки М₀, выполняется неравенство . Обозначается этот предел: .

Функция z = f (x, y) называется непрерывной в точке (x₀, y₀), если предел функции в этой точке равен значению функции в этой же точке, т.е.:

ПРИМЕР: Линейная функция  является непрерывной в любой точке (x₀, y₀).

Частные производные и дифференцируемость

Функции двух переменных

Пусть z = f (x, y) – функция двух переменных. Если зафикси­ровать один из аргументов этой функции, например, положить y = y₀, то получим функцию одной переменной z = f (x, y₀).

Частной производной функции z = f (x, y) в точке (x₀, y₀) по пе­ре­меной х называется обыкновенная производная функции          z = f (x, y₀), вычисленная в точке х₀. Такая частная производная обозначается:

Совершенно аналогично определяется частная производная по y:

ПРИМЕР: Для функции  можно записать:

Полным приращением функции z = f (x, y) в точке (x₀, y₀) назы­ва­ется величина:

Функция z = f (x, y) называется дифференцируемой в точке (x₀, y₀), если ее полное приращение в некоторой окрестности этой точки может быть представлено в виде:

,

где для функций α₁ и α₂ выполняются соотношения:

 и .

Дифференциалом функции z = f (x, y) называется выражение:

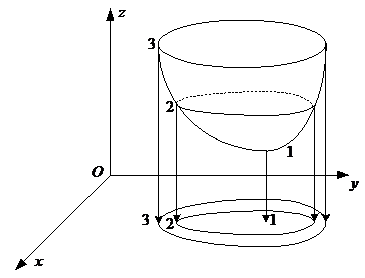
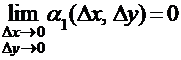Очевидно, что, как и в случае функции одной переменной, дифференциал функции двух переменных будет приближенно равен полному приращению функции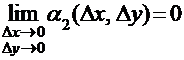.