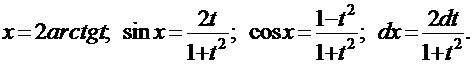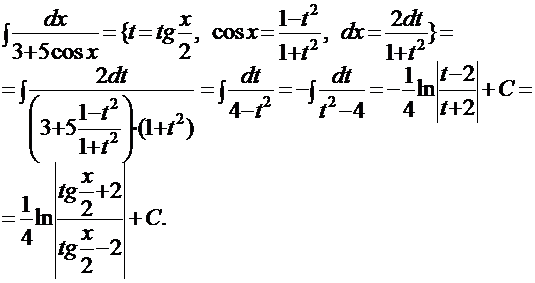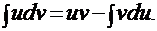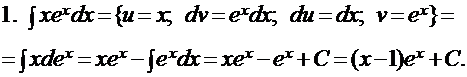Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод непосредственного интегрированияМетод вычисления неопределенных интегралов сличением с табличными интегралами, с использованием основных свойств неопределенных интегралов, а также тождественных преобразований подынтегральных функций называется методом непосредственного интегрирования. ПРИМЕРЫ: 1. Найти интеграл: Решение. Предложенный интеграл табличный (формула 14 таблицы при а = 4), поэтому можно записать:
2. Найти интеграл: Решение. Попытка сличения показывает, что данный интеграл табличным не является. Однако, принимая во внимание, что:
и используя табличные интегралы 9 и 10, получим:
Метод замены переменной Во многих случаях удачное введение новой переменной интегрирования позволяет свести операцию нахождения интеграла к непосредственному интегрированию. Такой метод называется методом замены переменной или методом подстановки. В основе метода замены переменной лежит формула:
В этой формуле
ПРИМЕРЫ:
Рациональной тригонометрической функцией от переменных sin x и cos x называется выражение, в котором над этими переменными производятся арифметические действия (сложение, вычитание, умножение и деление).
ПРИМЕР: Выражение
Интегрирование рациональных тригонометрических функций сводится к интегрированию рациональных дробей с помощью универсальной тригонометрической подстановки: 
при этом
ПРИМЕР:
Метод интегрирования по частям Пусть u = u (x) и v = v (x) – дифференцируемые функции, тогда можно записать: d(uv) = v∙du + u∙dv, или: u∙dv = d(uv) − v∙du, и окончательно получить формулу:
Метод интегрирования по частям и заключается в применении этой формулы. Эта формула позволяет свести вычисление первоначального интеграла в левой части формулы к вычислению интеграла в правой части формулы, который при удачном разделении подынтегрального выражения заданного интеграла на составные части u и dv может оказаться либо сразу табличным, либо более простым, чем исходный интеграл.
ПРИМЕРЫ:
|
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 271. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

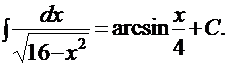
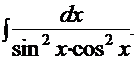
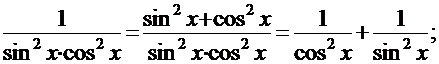
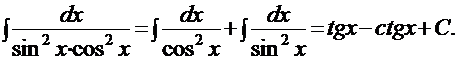
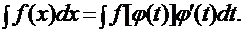
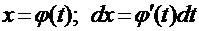 и есть замена переменной. В результате вычисления интеграла в правой части формулы получится функция, зависящая от аргумента t, поэтому, чтобы вернуться к первоначальной переменной х, нужно в полученном результате провести обратную замену
и есть замена переменной. В результате вычисления интеграла в правой части формулы получится функция, зависящая от аргумента t, поэтому, чтобы вернуться к первоначальной переменной х, нужно в полученном результате провести обратную замену 
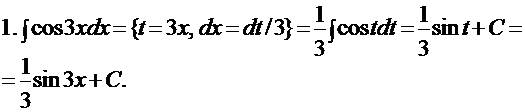
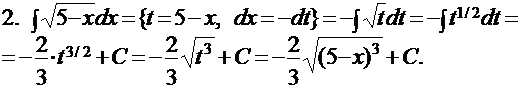
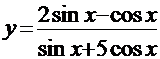 является рациональной тригонометрической функцией.
является рациональной тригонометрической функцией.