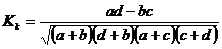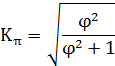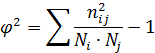Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема 9. КОРРЕЛЯЦИОННО – РЕГРЕССИОННЫЙ АНАЛИЗ ВЗАИМОСВЯЗЕЙ
Цель занятия – изучить возможности применения корреляционно-регрессионного анализа для количественных и качественных показателей Вопросы для обсуждения: 1. Охарактеризуйте этапы проведения корреляционно-регрессионного анализа. 2. Раскройте суть парной и множественной регрессии. 3. Как рассчитывается линейный коэффициент корреляции и коэффициент эластичности. 4. Перечислите критерии оценки тесноты связи между результативным и факторным признаками при помощи корреляции рангов. 5. При помощи каких показателей оценивается теснота связи между качественными признаками.
Методические указания Прямолинейная однофакторная модель связи
где а0, а1 – коэффициенты регрессии, они определяются при помощи метода наименьших квадратов:
или по сгруппированным данным:
где fx, fy –число единиц совокупности согласно распределению соответственно по факторному и результативному признакам. Расчет коэффициентов а0 и а1 осуществляется по следующим формулам:
Линейный коэффициент корреляции можно рассчитать по нескольким формулам:
Коэффициент ассоциации:
Коэффициент контингенции:
Коэффициент сопряженности Пирсона
где j2 – показатель взаимной сопряженности
где nij - частоты внутри клеток таблицы; i – номер строки; j – номер графы; Ni – итоговые частоты по строкам; Nj - итоговые частоты по графам.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 250. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
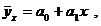
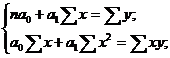
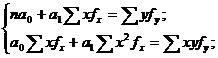
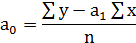
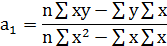
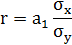
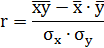
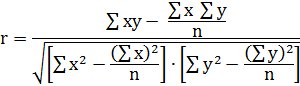

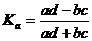 ,
,