
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
СРЕДНИЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ВАРИАЦИИ
Цель занятия - изучить методику расчета различных видов средних величин и показателей вариации. Вопросы для обсуждения: 1. Значение средних величин в статистических исследованиях. 2. Виды средних. 3. Средняя арифметическая, ее виды и основные свойства. 4. Средняя гармоническая, область ее применения. 5. Структурные средние, их значение в анализе. 6. Показатели асимметрии и эксцесса. 7. Назовите абсолютные показатели степени колеблемости значений признака. 8. Относительные показатели вариации, их значение и условия применения. 9. Определение дисперсии и назовите ее основные свойства. 10. Сформулируйте правило сложения дисперсий и условия его практического использования. 11. Что такое дисперсия альтернативного признака? Методические указания
Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Виды степенных средних величин: 1.Средняя арифметическая взвешенная:
где хi – вариант; fi – частота возникновения варианта. 2.Средняя гармоническая взвешенная:
где М = х ×f 3.Средняя квадратическая взвешенная:
4.Средняя геометрическая взвешенная:
Или где п – количество уровней ряда.
Виды структурных средних величин: 1.Мода интервального ряда распределения:
где хМо - нижняя граница модального интервала; hМо- величина модального интервала;
2.Медиана интервального ряда распределения: 
где хМе - нижняя граница медианного интервала;
3. Квартиль ряда распределения: а) нижний (первый) квартиль
в) верхний (третий) квартиль
где
4.Дециль ряда распределения: а) нижний (первый) дециль
в) верхний (девятый) дециль
где
Вариация - колеблемость, изменяемость величины признака у единиц совокупности. Показатели вариации бывают абсолютные и относительные. Абсолютные показатели: 1.Размах вариации:
2.Среднее линейное отклонение взвешенное:
где 3.Дисперсия вариационного признака взвешенная:
4.Среднее квадратическое отклонение вариационного признака взвешенное:
5.Дисперсия альтернативного признака:
где
6.Среднее квадратическое отклонение альтернативного признака:
Относительные показатели вариации: 1.Коэффициент осцилляции:
2.Линейный коэффициент вариации:
3.Коэффициент вариации:
Если коэффициент вариации равен или менее 33%, то исследуемая совокупность признается однородной. Правило сложения дисперсий для средней величины признака:
где
1. Общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака (хi) от общей средней величины (
где fo – частота общая в изучаемой совокупности. 2. Средняя из внутригрупповых дисперсий (остаточная дисперсия) отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки.
где
3. Межгрупповая дисперсия (факторная) характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки.
где Коэффициент детерминациипоказывает долю общей вариации изучаемого признака, обусловленную вариацией группировочного признака.
Корреляционное отношение показывает влияние признака, положенного в основу группировки, на вариацию результативного признака.
Коэффициент асимметрии:
Эксцесс:
где
Задачи для решения Задача 12.Имеются данные о заработной плате рабочих двух цехов, таблица 16:
Таблица 16 – Исходные данные
Определите среднюю заработную плату рабочих за каждый месяц и за два месяца вместе. Задача 13.Имеются данные о дневной продаже яблок в торговой точке города, таблица 17:
Таблица 17 – Исходные данные
Определите среднюю цену за 1 кг яблок. Укажите вид средней величины. Задача 14.Рассчитайте средний курс продажи одной акции по данным о торгах на фондовой бирже при условии, таблица 18:
Таблица 18 – Исходные данные
Каким видом средней величины Вы воспользовались и почему? Задача 15.Качество предприятия характеризуется следующими данными (за месяц), таблица 19: Таблица 19 – Исходные данные
Определите средний процент брака в целом по предприятию. Задача 16.Рассчитайте средний уровень издержек обращения на 100 рублей товарооборота и средний товарооборот при условии, таблица 20: Таблица 20 – Исходные данные
Задача 17.Распределение предпринимателей по стажу работы, таблица 21: Таблица 21 – Исходные данные
Определите средний стаж работы предпринимателей.
Задача 18.Имеются следующие данные о движении основных фондов по полной стоимости таблица 22: Таблица 22 – Исходные данные, тыс. руб.
Определите стоимость основных фондов на конец года; среднегодовую стоимость основных фондов (двумя способами) и объясните расхождение полученных результатов. Задача 19.Рассчитайте среднемесячный остаток оборотных средств за 2 квартал при условии, таблица 23:
Таблица 23 – Исходные данные
Каким видом средней величины Вы воспользовались и почему? Задача 20.Рассчитайте среднюю долю экспортной продукции при следующих данных, таблица 24:
Таблица 24 – Исходные данные
Какой вид средний величины Вы использовали и почему?
Задание 21.Определите среднюю годовую численность населения области при условии, таблица 25:
Таблица 25 – Исходные данные
Задание 22.По исходным данным задачи 9 рассчитать: 1) среднегодовой валовой региональный продукт на душу населения; 2) среднегодовые темпы роста валового регионального продукта на душу населения. Задача 23. Имеются данные о средненедельной заработной плате рабочих топливно-энергетической отрасли в одном из штатов США, таблица 26:
Таблица 26 – Исходные данные
Рассчитать среднюю заработную плату, найти моду и медиану аналитически и графически.
Задача 24. Распределение студентов одного из факультетов по возрасту характеризуется следующими данными, таблица 27:
Таблица 27 – Исходные данные
Вычислите структурные средние и изобразите их графически.
Задача 25. Имеются данные о распределении скважин в одном из районов бурения по глубине, таблица 28:
Таблица 28 – Исходные данные
Найдите структурные средние аналитически и графически. Задача 26. Имеются данные о чистой прибыли (балансовой за вычетом налогов) предприятий двух районов таблица 29: Таблица 29 – Исходные данные
По каждому району и по обоим районам вместе найти моду и медиану (аналитически и графически)
Задача 27. Имеется следующий ряд распределения телеграмм, принятых отделением связи, по числу слов, таблица 30: Таблица 30 – Исходные данные
Рассчитайте и изобразите графически структурные средние.
Задача 28. Имеются следующие данные о распределении сотрудников коммерческого банка по среднемесячной заработной плате, таблица 31: Таблица 31 – Исходные данные
Определите структурные средние. Задача 29. По данным задачи 23 рассчитать эксцесс, показатель асимметрии, а также построить их графически.
Задача 30. По данным задачи 24 вычислить абсолютные и относительные показатели вариации.
Задача 31. Средняя урожайность зерновых культур в двух районах за 2008-2012 гг. характеризуется следующими данными, ц/га, таблица 32: Таблица 32 – Исходные данные
Рассчитайте все показатели вариации. Определите, в каком районе урожайность зерновых культур более устойчива.
Задача 32. По данным задачи 25 определите дисперсию и среднее квадратическое отклонение глубины скважин, применяя способ отсчета от условного нуля.
Задача 33. По данным задачи 26 определить дисперсии чистой прибыли: 1) групповые (по каждому району); 2) среднюю из групповых; 3) межгрупповую; 4) общую.
Задача 34. По данным задачи 27 рассчитать абсолютные и относительные показатели вариации.
Задача 35. По данным задачи 28 определить все показатели вариации. Сделать выводы.
Задача 36. Имеются следующие выборочные данные о расходах на платные услуги домохозяйствами района, таблица 33:
Таблица 33 – Исходные данные
Определить для домохозяйств района дисперсии: 1) групповые (по каждому району); 2) среднюю из групповых; 3) межгрупповую; 4) общую.
Задача 37. Имеются следующие выборочные данные о вкладах населения района, таблица 34:
Таблица 34 – Исходные данные
Определите тесноту связи между средним размером вклада и типом населения, исчислив эмпирическое корреляционное отношение, эмпирический коэффициент детерминации.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 368. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
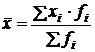 .
.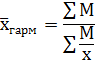
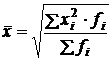 .
.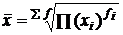
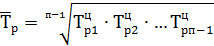
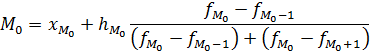
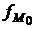 - частота модального интервала;
- частота модального интервала;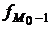 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;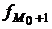 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.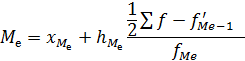
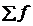 - сумма частот;
- сумма частот;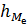 - частота медианного интервала;
- частота медианного интервала;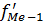 - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному; - частота медианного интервала.
- частота медианного интервала.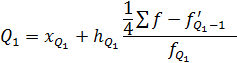
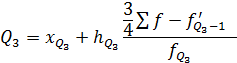
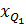 ,
, 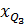 - нижняя граница квартильного интервала;
- нижняя граница квартильного интервала;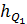 ,
, 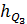 - величина квартильного интервала;
- величина квартильного интервала;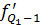 ,
, 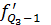 - накопленная частота интервала, предшествующего квартильному;
- накопленная частота интервала, предшествующего квартильному;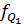 ,
, 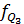 - частота квартильного интервала.
- частота квартильного интервала.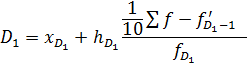
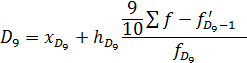

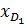 ,
, 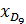 - нижняя граница децильного интервала;
- нижняя граница децильного интервала;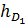 ,
, 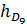 - величина децильного интервала;
- величина децильного интервала;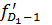 ,
, 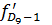 - накопленная частота интервала, предшествующего децильному;
- накопленная частота интервала, предшествующего децильному;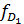 ,
, 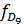 - частота децильного интервала.
- частота децильного интервала. .
.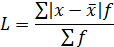
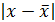 - абсолютное значение отклонений.
- абсолютное значение отклонений.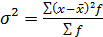
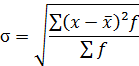
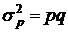
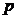 - доля единиц в совокупности, обладающих данным признаком;
- доля единиц в совокупности, обладающих данным признаком;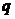 - доля единиц, не обладающих данным признаком.
- доля единиц, не обладающих данным признаком.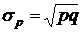 .
.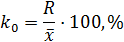
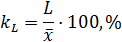
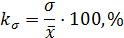
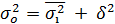
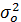 - общая дисперсия;
- общая дисперсия;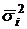 - средняя из внутригрупповых дисперсий;
- средняя из внутригрупповых дисперсий;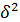 - межгрупповая дисперсия.
- межгрупповая дисперсия.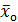 ) и может быть вычислена как:
) и может быть вычислена как: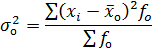
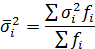
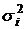 - групповые дисперсии; fi - число единиц в группах.
- групповые дисперсии; fi - число единиц в группах.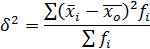
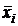 - групповые средние;
- групповые средние; 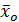 - общая средняя.
- общая средняя.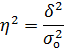
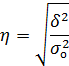

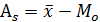
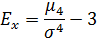
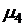 - центральный момент четвертого порядка, определяемый по формуле:
- центральный момент четвертого порядка, определяемый по формуле: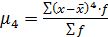 .
.