
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Экспериментально-статистическое исследование связей⇐ ПредыдущаяСтр 19 из 19 Главная задача всякого научного исследования заключается в изучении связей между явлениями, параметрами и факторами. Связи бывают функциональными и вероятностными (статистическими). В первом случае каждому значению входной величины соответствует одно или несколько строго определенных значений выходной. Статистические связи проявляются лишь при многократном испытании. При этом данному значению входной величины соответствует множество значений выходной. Корреляционный анализ Корреляционный анализ — один из широко распространенных методов оценки статистических связей. Он отвечает на вопросы: влияет ли данная входная величина на выходную и какова степень (теснота) связи между величинами? Предположим, что в результате эксперимента, цель которого — изучить влияние фактора x на параметр y, получены данные в виде совокупностей значений х и y, объемом n каждая, причем каждому значению xі соответствует определенное значение yi. Каждую пару величин можно представить точкой на поле координат xОy. Совокупность точек образует диаграмму рассеивания, рис. 7.1. По такой диаграмме можно судить о тесноте связи между величинами, однако подобная оценка субъективна. Числовой характеристикой связи служит корреляция — математическое ожидание произведения отклонений x и y от их математических ожиданий: Оценка корреляции по опытным данным: Размерность полученной величины равна произведению размерностей величин x и y, что затрудняет анализ тесноты связи. Поэтому чаще используют безразмерный коэффициент корреляции, равный  или для результатов опыта оценку коэффициента корреляции:
Выясним, как связано значение коэффициента корреляции с видом диаграммы рассеяния. Рассмотрим такие случаи: 1) Точки рассеяны в некоторой области, симметричной относительно вертикальной и горизонтальной прямых с уравнениями Поскольку точки рассеяны таким образом, что количество точек в каждом квадранте приблизительно одинаково, сумма (7.4) будет близка к нулю: 2) Между величинами x и y существует функциональная линейная зависимость вида где b и b0 — коэффициенты, рис. 7.1 б, в. Тогда Поскольку согласно (6.22) Sy = |b| Sx, Положительному значению b соответствует kxy = 1, рис. 7.1 б, а отрицательному — kxy = –1, рис. 7.1 в. Следовательно, если по результатам опытов получено значение kxy = ±1, можем утверждать, что между величинами x и y существует функциональная линейная зависимость. 3) Точки рассеяны в некоторой области, расположенной несимметрично относительно прямых с уравнениями Оба эти случая свидетельствуют о наличии статистической связи между величинами x и y. Возможны случаи, когда между величинами существует статистическая или даже функциональная связь, но в некотором интервале значений этих величин их коэффициент корреляции будет близок к нулю. Например, между величинами x и y на рис. 7.1 е существует явная функциональная связь, но Таким образом, коэффициент корреляции дает оценку не только наличия связи между величинами, но и степени ее линейности. Регрессионный анализ Целью регрессионного анализа является установление аналитической зависимости между выходной и входными величинами по данным экспериментальных исследований. Известно, что в общем случае зависимость между величинами может быть представлена таблично, графически и аналитически. Табличный способ позволяет определить значение выходной величины для заданных значений входных, но не дает представления о характере зависимости. Графический способ создает наглядность представления зависимости, позволяет визуально оценить ее характер. Аналитическая зависимость позволяет исследовать функцию методами математического анализа, т.е. определить значения максимума, минимума, точек перегиба и т.д. Получение аналитической зависимости желательно при разработке расчетных методик, в особенности при создании расчетных программ на ЭВМ. Эта зависимость наиболее универсальна, из нее просто получить табличную и графическую. Аналитические зависимости, полученные по данным эксперимента путем регрессионного анализа называются эмпирическими или аппроксимирующими. Необходимо иметь в виду, что если теоретические формулы, полученные на основе знания законов процесса, могут быть использованы при произвольных значениях аргументов, то эмпирические являются приближенными и могут применяться лишь в определенных условиях и в ограниченных пределах аргументов. Один и тот же процесс может быть описан несколькими различными эмпирическими формулами. В регрессионном анализе в отличие от корреляционного только выходные величины являются случайными. Входные должны быть неслучайными и некоррелированными между собой. Задача получения аналитической зависимости включает в себя три этапа: — выбор вида уравнения регрессии; — определение коэффициентов уравнения; — проверка адекватности установленной зависимости данным эксперимента. Первый этап является неформализованной процедурой. Здесь многое зависит от опыта исследователя. Уже отмечалось, что один и тот же процесс может быть описан различными эмпирическими зависимостями. На практике при выборе вида уравнения обычно руководствуются следующим. По данным эксперимента первоначально строят графическую зависимость. Ее сравнивают с различными кривыми, уравнения которых известны, и останавливаются на наиболее вероятной.
Если в результате построений окажется, что некоторые точки существенно отклоняются от общей зависимости, то следует проверить вычисления для них, а при необходимости повторить эксперимент. Если до обработки экспериментальных данных известна теория исследуемого процесса, в основу эмпирической зависимости желательно положить функциональную зависимость, определяемую этой теорией. Например, известно, что теоретическая напорная характеристика турбомашины является прямой линией, а потери напора в турбомашине пропорциональны квадрату расхода. Поэтому для описания экспериментальной напорной характеристики наиболее целесообразна ориентация на квадратичные зависимости. После выбора вида зависимости определяют коэффициенты, входящие в эту зависимость. В общем виде задачу можно сформулировать следующим образом. Исследуется зависимость параметра y от факторов x1, x2, …, xk. Проведено n серий опытов при различных сочетаниях уровней факторов; в каждой серии для u-го сочетания уровней факторов получена выборка значений параметра y, определено среднее выборочное которая содержит m неизвестных параметров (коэффициентов, показателей степеней и др.) b1, b2, …, bm. Задача состоит в определении такого сочетания этих параметров, при котором значения y, рассчитанные по зависимости (7.5), будут наиболее близки к экспериментальным данным В настоящее время выполнение такой задачи не представляет трудности, поскольку существуют программы для ЭВМ, предназначенные для поиска аппроксимационых зависимостей и определения их коэффициентов. Наиболее распространенным методом поиска коэффициентов уравнений регрессии является метод наименьших квадратов. Метод заключается в поиске минимума функции где Рассмотрим случай поиска линейной однофакторной зависимости вида для совокупности экспериментальных данных, представленной на рис. 7.2 а. Функция Ф в данном случае есть функция двух переменных: Функция будет иметь минимум, если ее частные производные по обоим переменным будут равны нулю Преобразовав выражения, получим систему двух линейных уравнений Решив систему, найдем значения коэффициентов уравнения регрессии. В практике математической обработки опытных данных широко используются нелинейные формулы, достаточно просто преобразуемые к линейному виду. К ним относятся параболические и степенные зависимости. Распространенная в гидравлическом эксперименте параболическая зависимость вида Степенные зависимости вида где C — коэффициент, b1, b2, …, bk — показатели степени, приводятся к полиномиальному виду путем логарифмирования: Обозначив b0 = Ln C — свободный член полинома, и прологарифмировав значения факторов и параметра, можем применить метод наименьших квадратов для поиска значений b0, b1, b2, …, bk. Проверка соответствия установленной зависимости экспериментальному материалу (проверка адекватности) включает в себя три этапа. 1. Ищется остаточная дисперсия, или дисперсия адекватности где fад = n – m — количество степеней свободы, равное разности количества опытов n и количества коэффициентов в уравнении регрессии m. Дисперсия адекватности будет тем меньше, чем лучше совпадают расчетные значения параметра 2. Определяется дисперсия воспроизводимости, показывающая точность определения параметра в опыте. В случае, если для каждого сочетания уровней факторов проводилось несколько параллельных опытов, ищутся дисперсии Если параллельные опыты не проводятся, то в качестве средневзвешенной дисперсии принимается где ΔYпред — предельная абсолютная погрешность определения выходной величины, определяемая по классу прибора и с доверительной вероятностью 0,955 равная двум среднеквадратическим отклонениям измеряемой величины. 3. Проверяется однородность дисперсий адекватности и воспроизводимости где Если расчетное значение критерия Фишера окажется меньше табличного, то полученное уравнение регрессии адекватно эксперименту с уровнем значимости α. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 694. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (7.1)
, (7.1) . (7.2)
. (7.2) , (7.3)
, (7.3) . (7.4)
. (7.4)
 и
и  , рис. 7.1 а. Эти прямые делят плоскость xОy на четыре квадранта. Произведение
, рис. 7.1 а. Эти прямые делят плоскость xОy на четыре квадранта. Произведение  в I и III квадрантах будет иметь знак (+), а во II и IV — знак (–).
в I и III квадрантах будет иметь знак (+), а во II и IV — знак (–). . Это говорит о том, что, по-видимому, связь между величинами x и y отсутствует.
. Это говорит о том, что, по-видимому, связь между величинами x и y отсутствует. ,
, и
и  . Подставив последнее выражение в (7.4), получим
. Подставив последнее выражение в (7.4), получим .
.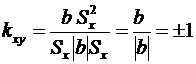 .
.
 и дисперсия
и дисперсия  . Для поиска аппроксимационной зависимости выбрана некоторая функция вида
. Для поиска аппроксимационной зависимости выбрана некоторая функция вида , (7.5)
, (7.5) , (7.6)
, (7.6) — значение параметра y, полученное расчетом по зависимости (7.5) для u-го сочетания уровней факторов. Функция (7.6) характеризует степень расхождения расчетных значений и опытных данных. Наилучшим будет такое сочетание коэффициентов, при котором это расхождение будет минимальным. Следовательно, задача сводится к поиску минимума функции Ф и может быть решена методом математического анализа.
— значение параметра y, полученное расчетом по зависимости (7.5) для u-го сочетания уровней факторов. Функция (7.6) характеризует степень расхождения расчетных значений и опытных данных. Наилучшим будет такое сочетание коэффициентов, при котором это расхождение будет минимальным. Следовательно, задача сводится к поиску минимума функции Ф и может быть решена методом математического анализа. , (7.7)
, (7.7) . (7.6)
. (7.6) ;
; .
.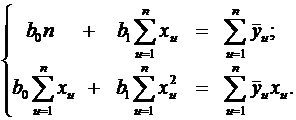 (7.7)
(7.7) приводится к линейному виду подстановкой z = x2. Коэффициенты полученного линейного уравнения
приводится к линейному виду подстановкой z = x2. Коэффициенты полученного линейного уравнения  находятся по описанной методике.
находятся по описанной методике. , (7.8)
, (7.8) , (7.8)
, (7.8) , (7.6)
, (7.6) по зависимости (6.39), которая и принимается в качестве дисперсии воспроизводимости
по зависимости (6.39), которая и принимается в качестве дисперсии воспроизводимости  .
. , (7.6)
, (7.6) , (7.1)
, (7.1) — количество степеней свободы дисперсии воспроизводимости; nп u — количество параллельных опытов для u-го сочетания уровней факторов.
— количество степеней свободы дисперсии воспроизводимости; nп u — количество параллельных опытов для u-го сочетания уровней факторов.