
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Погрешности косвенных измеренийЧасто интересующая нас величина непосредственно не может быть измерена, а определяется как функция других величин, которые находятся опытным путем. Например, расход воздуха в прямоугольном канале где h и b — высота и ширина канала; vср — средняя скорость воздуха. Для определения расхода измеряют ширину, высоту канала и среднюю скорость воздуха. При измерениях этих величин допускаются погрешности. Оценка их может быть выполнена по рассмотренной методике. Погрешность определяемой величины зависит от погрешностей измеряемых величин и от вида функциональной связи между ними. Предположим, что величина, погрешность которой необходимо определить, является произвольной функцией k измеряемых переменных Поставив ряд параллельных опытов, найдем оценки Распространив свойство (6.17) математического ожидания на его оценку, можем утверждать, что Представим случайные величины xi в виде Если функция φ непрерывна и во всех точках интересующего нас интервала имеет производные, то ее, можно разложить в ряд Тейлора. Выполним эту операцию и оставим в ряде только линейные члены: С учетом (6.26) и (6.27)  Возведем правую и левую части последнего равенства в квадрат и найдем математические ожидания левой и правой частей: Левая часть равенства есть дисперсия y (6.19). Раскрыв скобки в правой части, получим или, с учетом свойств (6.15) и (6.16) математического ожидания Поскольку математическое ожидание квадрата отклонения случайной величины от ее математического ожидания есть дисперсия, а математическое ожидание произведения отклонений двух величин есть их корреляция, для независимых случайных величин равная нулю,
Заменив дисперсии xi их оценками по выборке Например, для случая (6.25) В случае, если точность измерения параметров h и b значительно выше, чем точность измерения vср, погрешностями этих величин можем пренебречь. Тогда |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 494. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
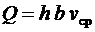 , (6.26)
, (6.26)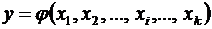 , (6.27)
, (6.27)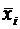 и
и 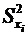 математического ожидания mxi и дисперсии Dxi для каждой i-й величины. Необходимо определить оценки
математического ожидания mxi и дисперсии Dxi для каждой i-й величины. Необходимо определить оценки 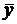 и
и 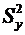 математического ожидания my и дисперсии Dy для искомой величины.
математического ожидания my и дисперсии Dy для искомой величины.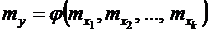 и
и 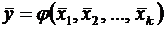 . (6.28)
. (6.28)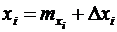 , где Δxi — отклонение величины от ее математического ожидания.
, где Δxi — отклонение величины от ее математического ожидания.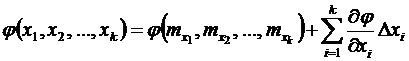 .
.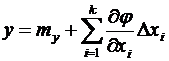 или
или 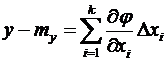
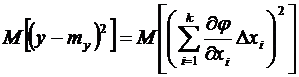
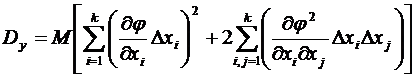 ,
,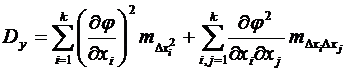 .
.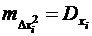 и
и 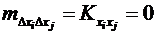 , получим
, получим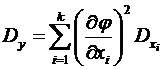 . (6.29)
. (6.29)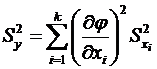 . (6.30)
. (6.30)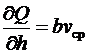 ,
, 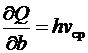 и
и 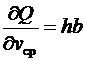 . Тогда
. Тогда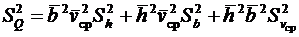 .
.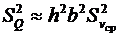 .
.