
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сравнение выборочных средних. Дисперсионный анализ.В ходе исследований часто возникает необходимость сравнения резуль-татов измерения, представленных двумя выборками (например, производительность новой машины сравнивается с базовым вариантом). Сравнивая выборочные средние, нужно быть уверенным, что разница между ними значима, т.е. вызвана изменениями в конструкции машины, а не является результатом погрешностей опытов. Таблица 6.4 – Значения критерия Gα (f1, f2) при уровне значимости α = 0,05
Пусть для каждой из выборок определены выборочные средние  Поскольку выборочные средние есть случайные величины, величина Z также случайна. Доверительный интервал для этой величины где mZ и SZ – математическое ожидание и среднеквадратическое отклонение Z. Исходя из выражения (6.36) с учетом свойств (6.21) и (6.25) дисперсии, дисперсия Z составит где Предположим, что различие между Следовательно, если Z выходит за пределы указанного интервала, можем утверждать, что различие между выборочными средними Критерий tf,α берется для соответствующего уровня значимости и суммарного числа степеней свободы двух дисперсий f = n1 + n2 – 2. Если эксперимент проводится с целью аппроксимации зависимости некоторого параметра от одного или нескольких факторов, необходимо определить значимость влияния каждого из факторов на параметр. Такая процедура называется дисперсионным анализом. Предположим, что необходимо установить, влияет ли изменение в заданном интервале фактора x на параметр y. Установим m уровней фактора. На каждом уровне поставим по n параллельных опытов и определим выборочное среднее и дисперсию значений y для каждого уровня: где yui — значение y, измеренное в i-м опыте из серии опытов, проведенных при u-м уровне фактора x. Результаты сведем в табл. 6.5. Если дисперсии Таблица 6.5 – Данные для дисперсионного анализа
Рассмотрим совокупность выборочных средних Дисперсия — дисперсии однородны, следовательно изменение выборочных средних обусловлено случайными погрешностями, а влияние фактора — не значимо. В противном случае — дисперсии неоднородны, и можем утверждать, что фактор x оказывает значимое влияние на параметр. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 510. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
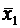 ,
, 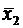 и дисперсии
и дисперсии 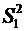 и
и 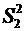 , причем дисперсии выборок однородны (в противном случае сравнивать выборочные средние нельзя!). Обозначим разницу между выборочными средними
, причем дисперсии выборок однородны (в противном случае сравнивать выборочные средние нельзя!). Обозначим разницу между выборочными средними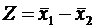 . (6.36)
. (6.36)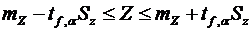 ,
,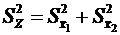 или
или 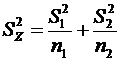 , (6.38)
, (6.38)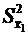 и
и 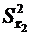 – дисперсии выборочных средних; n1 и n2 – объемы первой и второй выборок.
– дисперсии выборочных средних; n1 и n2 – объемы первой и второй выборок.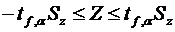 , или
, или 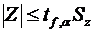 . (6.37)
. (6.37)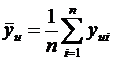 и
и 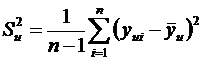 , (6.38)
, (6.38) однородны, что проверяется по критерию Кохрена, то можем определить средневзвешенную дисперсию погрешностей всех выборок:
однородны, что проверяется по критерию Кохрена, то можем определить средневзвешенную дисперсию погрешностей всех выборок: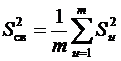 . (6.39)
. (6.39)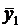
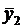

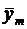
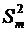
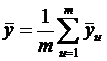 и
и 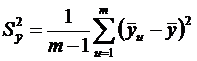 . (6.40)
. (6.40)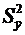 обусловлена двумя факторами: погрешностями определения выборочных средних
обусловлена двумя факторами: погрешностями определения выборочных средних  . Если
. Если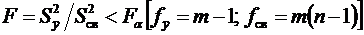 , (6.40)
, (6.40)