
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Числовые характеристики случайных величинФункции распределения вероятностей случайных величин хотя и являются их полной характеристикой, но не всегда удобны в для практического использования. Например, для получения графика функции распределения вероятностей по опытным данным необходимо провести несколько десятков измерений, что не всегда оправдано. Поэтому для описания случайных величин используют числовые характеристики, которые не являются их полным описанием, но достаточны для решения большинства практических задач. Математическое ожидание случайной величины характеризует положение центра группирования ее реализаций в генеральной совокупности. Математическое ожидание для дискретных и непрерывных случайных величин находятся по зависимостям: Математическое ожидание обладает следующими свойствами: 1. Математическое ожидание постоянной величины равно этой величине: 2. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин: 3. Математическое ожидание произведения нескольких случайных величин равно произведению математических ожиданий этих величин: 4. Математическое ожидание функции одной или нескольких случайных величин равно функции математических ожиданий этих величин:  Дисперсия случайной величины характеризует степень рассеяния ее реализаций вокруг математического ожидания и находится для дискретных и непрерывных случайных величин по зависимостям Формула (6.18) представляет собой математическое ожидание квадрата отклонения ΔX случайной величины от ее математического ожидания: Размерность дисперсии отличается от размерности самой случайной величины — равна квадрату ее размерности, — поэтому для удобства сравнения используют среднеквадратическое отклонение Дисперсия случайной величины обладает такими свойствами: 1. Дисперсия постоянной величины равна нулю: 2. Дисперсия суммы нескольких случайных величин равна сумме дисперсий этих величин: 3. Дисперсия произведения постоянной и случайной величин дисперсии случайной величины, умноженной на квадрат постоянной: 4. Дисперсия случайной величины равна разности математического ожидания квадрата случайной величины и квадрата математического ожидания этой величины: Оценкой для математического ожидания и дисперсии генеральной совокупности являются выборочное среднее и среднеквадратическое отклонение, определенные для выборки объемом n: где xi — i-е значение из выборки. Поскольку выборка из генеральной совокупности случайна, выборочное среднее также является случайной величиной, распределенной возле математического ожидания со среднеквадратическим отклонением, равным Из этого следует, что математическое ожидание можно определить с высокой точностью даже не особенно точными приборами. Но при этом необходимо выполнить большое число независимых измерений. Например, для повышения точности в 3 раза число опытов необходимо увеличить в 9 раз. Рациональнее для повышения точности результата использовать более точные приборы, уменьшив Sx. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 656. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  . (6.13)
. (6.13)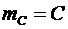 . (6.14)
. (6.14) . (6.15)
. (6.15)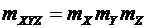 . (6.16)
. (6.16)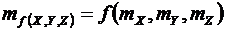 . (6.17)
. (6.17) и
и  . (6.18)
. (6.18)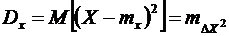 (6.19)
(6.19) размерность которого соответствует размерности самой величины. Используется также коэффициент вариации, равный отношению среднеквадратического отклонения к математическому ожиданию величины:
размерность которого соответствует размерности самой величины. Используется также коэффициент вариации, равный отношению среднеквадратического отклонения к математическому ожиданию величины:  , и показывающий относительную величину рассеяния.
, и показывающий относительную величину рассеяния. . (6.20)
. (6.20)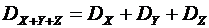 или
или  . (6.21)
. (6.21) или
или  . (6.22)
. (6.22) . (6.23)
. (6.23) и
и  , (6.24)
, (6.24) . (6.25)
. (6.25)