
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формулы для вычисления площади треугольника через радиусы. ⇐ ПредыдущаяСтр 6 из 6 Площадь треугольника (через радиус описанной окружности; через радиус вписанной окружности). 26. Вектор. Координаты вектора. Длина вектора. Определение. Вектор- это направленный отрезок имеющий начало и конец. Обозначается например Пусть А Тогда координатами вектора Длина вектора 27. Равные вектора. Коллинеарные вектора. Их свойства. Два вектора называются равными, если они коллиниарные и имеют одинаковую длину и направление.(равные вектора имеют равные координаты). Вектора называются коллинеарными, если существует прямая, которой они параллельны.
28. Коллинеарные вектора – это вектора, у которых координаты пропорциональны. Пусть вектор
29. Координаты середины отрезка. Если необходимо найти т. С ( 30. Расстояние между точками. 31. Алгебраические операции над векторами. Сумма векторов
Разность векторов (Построение) Разность векторов
Произведение вектора  32. Разложение вектора по двум неколлинеарным векторам. Теорема (о разложении вектора). Любой вектор 33. Скалярное произведение векторов, его свойства. Скалярное произведение векторов – называется произведение их длин на косинус угла между ними.
34. Условие перпендикулярности векторов. Два вектора перпендикулярны когда их скалярное произведение равно 0.
35. Нахождение угла между векторами.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 803. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. или
или 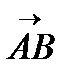 .
. - начало вектора и B
- начало вектора и B  - конец вектора
- конец вектора называются
называются  , где
, где  ,
, 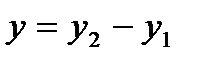 ;
; .
. - вектор
- вектор 
 , тогда
, тогда .
.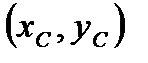 ,середину отрезка АВ,(т.А
,середину отрезка АВ,(т.А  , т.B
, т.B  ), тогда координата точки С
), тогда координата точки С 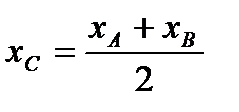 ,
,  .
. (обозначения смотри выше).
(обозначения смотри выше). и
и  называется вектор идущий из начала вектора
называется вектор идущий из начала вектора  .
.
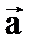 и
и  .
. на число
на число  - это коллинеарный ему вектор
- это коллинеарный ему вектор  , со направленный с вектором
, со направленный с вектором  .
. по определению
по определению в координатной форме.
в координатной форме.
 =
=  .
.