
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема 1. Теорема косинусов –квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Следствие 1.Следствие из теоремы косинусов (о связи диагоналей и сторон параллелограмма).Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. d12 + d22 = 2 a2 + 2 b2 Следствие 2.Следствие из теоремы косинусов об определении вида треугольника. Пусть с- наибольшая сторона треугольника. Если с2=а2+b2, то угол против с=90 градусов и треугольник прямоугольный. Если с2<а2+b2, то угол против с<90 градусов и треугольник остроугольный. Если с2>а2+b2, то угол против с>90 градусов и треугольник тупоугольный. Формула 1.Формулы для вычисления длины медианы треугольника.
Формула 2.
9. Теорема синусов. Следствие теоремы синусов( о радиусе описанной окружности).
Теорема 1. Теорема синусов – стороны треугольника пропорциональны синусам противолежащих углов.
где Следствие 1.Следствие из теоремы синусов (о радиусе описанной окружности). Диаметр описанной окружности около треугольника равен отношению стороны треугольника к синусу противоположного угла.
где 10. Свойства прямоугольного треугольника Теорема Пифагора. В любом прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Синус угла х – это отношение противолежащего катета к гипотенузе. Косинус угла х– это отношение прилежащего катета к гипотенузе.  Тангенс угла х – это отношение противолежащего катета к прилежащему. Котангенс угла х – это отношение прилежащего катета к противолежащему.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 810. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 стороны треугольника и угол
стороны треугольника и угол  , противолежащий стороне
, противолежащий стороне  .
.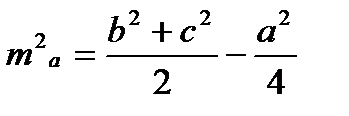 или
или 
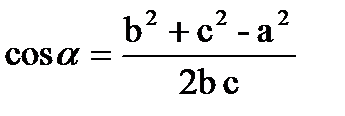 , угол
, угол  лежит напротив стороны а.
лежит напротив стороны а.
 ,
,  ,
,  — стороны треугольника,
— стороны треугольника,  — соответственно противолежащие им углы.
— соответственно противолежащие им углы.
 — радиус окружности, описанной вокруг треугольника.
— радиус окружности, описанной вокруг треугольника.