
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Часть 2 «Тела вращения. Многогранники»Стр 1 из 6Следующая ⇒ Часть 1 «Основы стереометрии»
1. Расстояние от точки до прямой; до плоскости. Определение 1. Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую. Определение 2.Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из заданной точки к заданной плоскости. 2. Свойство точки равноудаленной от сторон многоугольника; от вершин многоугольника. Свойство 1. Если через центр вписанной в многоугольник окружности проведена прямая перпендикулярная плоскости многоугольника, то все точки этой прямой равноудалены от сторон многоугольника. Свойство 2. Если через центр описанной около многоугольника окружности проведена прямая перпендикулярная плоскости многоугольника, то все точки этой прямой равноудалены от вершин многоугольника. 3. Угол между прямыми в пространстве. Определение. Угломмеждупрямымивпространстве будем называть любой из углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. 4. Угол между прямой и плоскостью. Определение. Углом между прямой и плоскостьюназывается угол между прямой и ее проекцией на эту плоскость. 5. Угол между плоскостями. Определение. Двугранный уголмеждуплоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.( Величиной угламеждуплоскостями называется величина меньшего двугранного угла). 6. Признак параллельности прямых. Теорема. (Признак) Если две прямые в пространстве параллельны третьей прямой, то они параллельны. 7. Признак параллельности прямой и плоскости.  Теорема.(Признак). Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
8. Признак параллельности плоскостей. Теорема(Признак).Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. 9. Теорема о двух плоскостях пересеченных третьей. Теорема. Если две параллельные плоскости пересекаются третьей плоскостью, то прямые образованные этим пересечением параллельны. 10. Признак перпендикулярности плоскостей. Теорема. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. 11. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ. 12. Теорема о трех перпендикулярах. Теорема.Прямая, лежащая в плоскости и перпендикулярная проекции наклонной к этой плоскости, перпендикулярна и самой наклонной. 13. Теорема о площади ортогональной проекции. Теорема. Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции. Часть 2 «Тела вращения. Многогранники» 1. Куб– Правильная четырехугольная призма, каждая грань которого представляет собой квадрат. Диагональ грани Диагональ куба Площадь полной поверхности Площадь боковой поверхности Объем 2. Параллелепипед – Четырехугольная призма, каждая грань которого представляет собой параллелограмм. Площадь полной поверхности Площадь боковой поверхности h — высота Объем Прямоугольный параллелепипед (прямая четырехугольная призма) каждая гранькоторой является прямоугольником. ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД - этопараллелепипед, боковые рёбра которого перпендикулярны основанию. 3. Призма — это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани — параллелограммами. Площадь полной поверхности Площадь боковой поверхности Объем Прямая призма -этопризма, боковые рёбра которого перпендикулярны основанию. Правильная призма-это призма, основанием которой является правильный многоугольник. Наклонная призмаПлощадь боковой поверхности Площадь боковой поверхности наклонной призмы Площадь боковой поверхности 4. Пирамида — многогранник, основание которого —многоугольник, а остальные грани — треугольники, имеющие общую вершину. Боковая поверхность — это сумма площадей боковых граней: Полная поверхность — это сумма площади боковой поверхности и площади основания: Объем Правильная пирамида -это пирамида, основанием которой является правильный многоугольник, а высота проецируется в центр этого многоугольника. Площадь боковой поверхности в правильной пирамиде
где
5. Усеченная пирамида− это многогранник, заключенный между основанием пирамиды и сечением, параллельным основанию. Площадь полной поверхности S = Sбок + S1 + S2 Объем усеченной пирамиды Правильной усеченной пирамидой называется часть правильной пирамиды. Площадь боковой поверхности правильной усеченной пирамиды 6. Цилиндр − это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Цилиндрическая поверхность образуется движением прямой параллельно самой себе. Указанная прямая являетсяобразующей цилиндрической поверхности. Площадь боковой поверхности прямого кругового цилиндра Площадь полной поверхности прямого кругового цилиндра Объем прямого кругового цилиндра 7. Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга,—вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности. Площадь боковой поверхностиконуса(площадь сегмента) Площадь полной поверхностиконуса Объемконуса 8. Усеченный конус− это геометрическое тело, заключенное между основанием конуса и сечением, параллельным основанию. Объем и площадь боковой поверхности усеченного конуса находятся по формулам Площадь полной поверхности 9. Сферической, поверхностью называется геометрическое место точек пространства, равноудаленных от одной точки. Шар — это тело ограниченное сферической поверхностью. Площадь сферы
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 773. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |




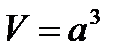
 , где Sо — площадь основания.
, где Sо — площадь основания.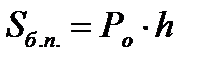 , где Ро — периметр основания,
, где Ро — периметр основания, .
. , где
, где  — периметр перпендикулярного сечения, l–длина бокового ребра.
— периметр перпендикулярного сечения, l–длина бокового ребра. , где
, где  — площадь перпендикулярного сечения, l–длина бокового ребра.
— площадь перпендикулярного сечения, l–длина бокового ребра. , где
, где  — периметр перпендикулярного сечения, l–длина бокового ребра.
— периметр перпендикулярного сечения, l–длина бокового ребра.
 , где h — высота, Sо — площадь основания.
, где h — высота, Sо — площадь основания.
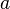 — апофема ,
— апофема ,  — периметр основания.
— периметр основания. .
. SоснH =
SоснH =  πR2H.
πR2H. где h — высота усеченного конуса,
где h — высота усеченного конуса, 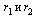 — радиусы оснований, l — длина образующей усеченного конуса.
— радиусы оснований, l — длина образующей усеченного конуса.