
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Формула 2.Для радиуса окружности, вписанной в правильный n-угольник.
21. Правильный четырехугольник. Диагональ Площадь квадрата (через сторону; через диагональ). Радиус вписанной окружности Радиус описанной окружности 22. Правильный треугольник Высота
23. Правильный шестиугольник Большая диагональ равна Формула для нахождения величины угла правильного многоугольника. Величина угла правильного многоугольника равна Площадь правильного шестиугольника.
24. Определение равновеликих фигур. Определение. Фигуры называется равновеликими – если их площади равны. 25. Формулы для вычисления площади: Площадь прямоугольника (через сторону; через диагональ). Площадь параллелограмма (через высоту; через угол; через диагонали). Площадь ромба (через угол; через диагонали; через высоту). Площадь трапеции. Площадь выпуклого четырехугольника. Площадь правильного треугольника. Площадь правильного шестиугольника.
Площадь треугольника (через две стороны и угол между ними) равна половине произведения сторон треугольника и на синус угла между ними. Площадь треугольника (через высоту) равна половине произведения основания на высоту. Площадь треугольника (формула Герона). Площадь квадрата (через сторону; через диагональ). Площадь круга. Площадь кругового сектора. Площадь кругового сегмента. Площадь описанного многоугольника |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 897. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


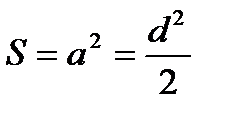

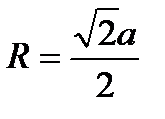 .
.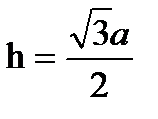
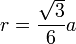 ,
, 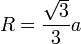

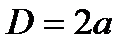 , меньшая
, меньшая 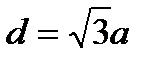 ,
, 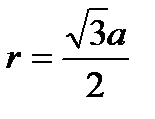 ,
, 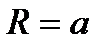 .
.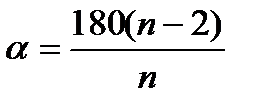 .
.

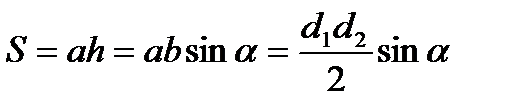

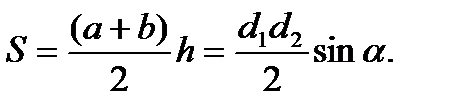
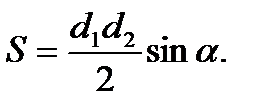
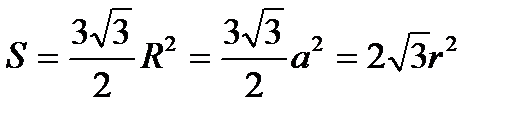
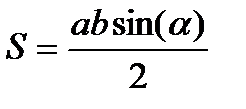
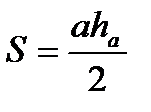 .
.
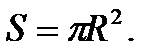
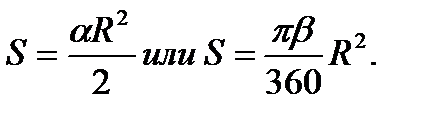 (
( 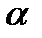 -угол в радианах,
-угол в радианах, 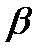 угол в градусах )
угол в градусах )
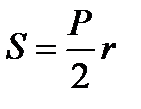 .
.