
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Объём шара, ограниченного сферой
Часть 3 «Основы планиметрии» 1. Внешний угол треугольника. Определение. Свойство.
Определение. Внешний угол – угол, дополняющий внутренний угол до 180 градусов. Свойство: 1. Величина внешнего угла треугольника равна сумме величин двух внутренних углов треугольника не смежных с ним.
2. Теорема о сумме углов треугольника. Следствие из теоремы. Теорема. Сумма углов треугольника равна 180 градусов. Следствие.1. У любого треугольника хотя бы 2 угла острых. Следствие.2.Величина внешнего угла равна сумме величин двух внутренних углов треугольника не смежных с ним. Следствие.3.Сумма внешних углов равна 360 градусов.
3. Определение средней линии треугольника. Свойства средней линии треугольника. Определение 1. Средняя линия треугольника– отрезок соединяющий середины двух его сторон. Свойство: 1. Средняя линия параллельна одной из его сторон(основанию)и равна половине этой стороны.
Определение медианы, биссектрисы и высоты треугольника. Определение 2. Медиана треугольника –отрезок концы которого соединяют вершины треугольника и середину противоположной стороны. Определение 3. Биссектриса треугольника– это отрезок биссектрисы угла, от вершины до точки пересечения с противоположной стороной. Определение 4. Высота треугольника- это перпендикуляр, опущенный из любой вершины на противоположную сторону или ее продолжение.
4. Свойства биссектрисы угла треугольника. Формула для вычисления длины биссектрисы треугольника. Свойство: 1. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам .  Свойство: 2. Биссектрисы треугольника пересекаются в одной точке (центр вписанной окружности) Свойство: 3. Биссектриса равноудалена от сторон треугольника. Формула для вычисления величины биссектрис:
x, y отрезки на которые биссектриса разбивает третью сторону.
5. Свойства медианы треугольника. Формула для вычисления длины медианы треугольника.
Свойство: 1. Медианы пересекаются в одной точке. (центр тяжести) Свойство: 2.Точкой пересечения медианы делятся в отношении 2:1 считая от вершины. Свойство: 3. Каждая медиана делит треугольник на два равновеликих треугольника. Свойство: 4. Три медианы делят треугольник на шесть равновеликих треугольника. Формула для вычисления величины медианы:
6. Центр вписанной и центр описанной окружности.
Определение 1.Если все стороны треугольника касаются окружности, то окружность называется вписанной в треугольник, а треугольник – описанным около этой окружности. Теорема 1. В любой треугольник можно вписать окружность и при этом только одну. Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.
Определение 2.Если все вершины многоугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник – вписанным в эту окружность. Теорема 2. Около любого треугольника можно описать окружность и при этом только одну. Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.
7. Отношение периметров, площадей, высот подобных фигур.
Свойство 1.Отношение периметров и высот подобных фигур равно коэффициенту подобия Свойство 2.Отношение площадей подобных фигур равно квадрату коэффициента подобия 8. Теорема косинусов. Следствия: связь между диагоналями и сторонами параллелограмма; определение вида треугольника; формула для вычисления длины медианы треугольника; вычисление косинуса угла треугольника. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 554. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
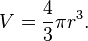
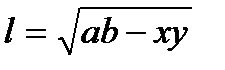 , где а,b стороны «прилежащие» к биссектрисе
, где а,b стороны «прилежащие» к биссектрисе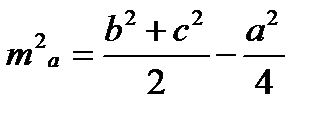 или
или  , где а,b, с стороны треугольника.
, где а,b, с стороны треугольника.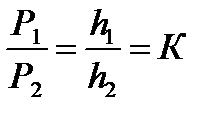
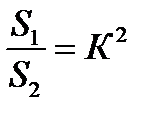 .
.