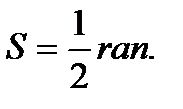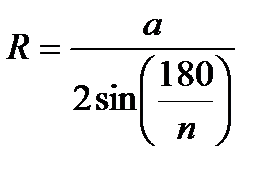Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойство высоты прямоугольного треугольника, опущенного на гипотенузу.Свойство: 1. В любом прямоугольном треугольнике, высота, опущенная из прямого угла( на гипотенузу), делит прямоугольный треугольник, на три подобных треугольника. Свойство: 2. Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу(или среднему геометрическому тех отрезков на которые высота разбивает гипотенузу). Свойство: 3. Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу. Свойство: 4. Катет против угла в 30 градусов равен половине гипотенузы. Формула 1. Формула 2. Свойство: 5. В прямоугольном треугольнике медиана проведенная к гипотенузе, равна ее половине и равна радиусу описанной окружности. Свойство: 6. Зависимость между сторонами и углами прямоугольного треугольника:
11. Свойство диаметра перпендикулярного хорде. Свойство: 1. Диаметр перпендикулярный хорде делит эту хорду пополам. 12. Свойство дуг, заключенных между параллельными хордами. Свойство: 1. Дуги, заключенные между параллельными хордами, равны. 13. Свойства касательной. Определение. Касательная – прямая, имеющая только одну точку пересечения с окружностью. Свойство: 1. Касательная к окружности перпендикулярна к радиусу проведенного в точку касания. Свойство: 2. Две касательные проведенные из одной точки к окружности – равны. 14. Определение вписанного угла, центрального угла. Измерение их величин. Свойство вписанного угла, его связь с центральным углом, опирающимся на туже хорду.
Определение 1. Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность – вписанный угол.  Определение 2. Центральный угол в окружности – плоский угол с вершиной в ее центре.
Угол, вписанный в окружность, равен половине соответствующего центрального угла. Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла. Свойство: 1. Все вписанные углы, опираются на одну и ту же дугу, равны между собой. Свойство: 2. Вписанный угол, опирающийся на диаметр прямой. 15. Угол с вершиной внутри круга; угол с вершиной вне круга; угол межу касательной и хордой. Измерение их величин.
Свойство: 1. Угол, вершина которого лежит внутри круга, измеряется полусуммой двух дуг, из которых одна заключается между его сторонами, а другая между продолжениями сторон. Свойство: 2. Угол, вершина которого лежит вне круга, измеряется полуразностью двух дуг, заключенных между его сторонами. Свойство: 3. Угол, составленный касательной и хордой, измеряется половиной дуги заключенной внутри него. 16. Свойство хорд, пересекающихся в круге. Свойство: 1. Если хорды, АВ и СD окружности пересекаются в точке S, то AS 17. Свойство секущей и касательной, проведенной из одной точки. Свойство: 1. Произведение отрезков секущей окружности равно квадрату отрезка касательной, проведенной из той же точки. 18. Свойство секущих, проведенных из одной точки. Если из одной точки P к окружности проведены две секущие, пересекающие окружность в точках A,B,C,D соответственно, то AP 19. Свойства вписанного и описанного четырехугольника. Свойство: 1. Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равна 180 градусов. Свойство: 2. Четырехугольник можно описать около окружности тогда и только тогда, когда суммы длин его противоположных сторон равны. 20. Правильный многогранник. Формулы для вычисления радиусов вписанной и описанной окружности. Определение 1.Правильныймногоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.Площадь правильного многоугольника Формула 1.Для радиуса окружности, описанной около правильного n-угольника. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 993. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
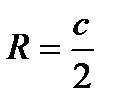 , где
, где  гипотенуза;
гипотенуза;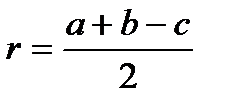 , где
, где 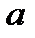 ,
, 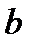 катеты.
катеты.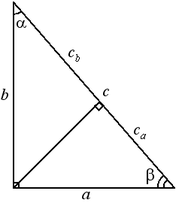
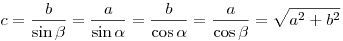 ;
;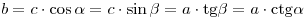 ;
;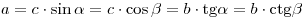 .
. ВS=DS
ВS=DS