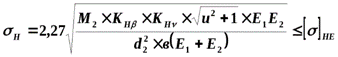Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
При расчете на контактную прочность зубьев принимаетсяNHO =30HB24 [1] . При расчете на изгиб зубьев для зубчатых колес, выполненных из сталей NFO = 4×106 , для зубчатых колес из других материалов NFO=3×106. При расчете NHE =NFE исходят из того, что за каждый оборот колеса каждый зуб испытывает один цикл нагружений NHE = NFE = 60×n ×T,
Из условия контактной прочности рабочих поверхностей зубьев:
1.6. Проверочный расчёт контактных напряжений на рабочих поверхностях зубьев
Червячная передача. геом. Параметры и расчет на прочность. Червячная передача –это зубчато-винтовая передача, движение в которой преобразуется по принципу винтовой пары с присущим ей повышенным скольжением. Червячные передачи применяют для передачи вращательного движения между валами, оси которых перекрещиваются в пространстве. Наиболее часто угол перекрещивания Θ составляет 90°. Ведущим (в большинстве случаев) является червяк, представляющий собой зубчатое колесо с малым числом (z1 = 1...4) зубьев (витков), похожее на винт Архимеда с трапецеидальной или близкой к ней по форме резьбой. Червячное колесо выполняется косозубым. Для увеличения длины контактных линий в зацеплении с червяком зубья червячного колеса в осевом сечении имеют форму дуги. делительный диаметр, т.е. диаметр такого цилиндра червяка, на котором толщина витка равна ширине впадины: d1 = m q, где: q – число модулей в делительном диаметре червяка или коэффициент диаметра червяка. С целью сокращения номенклатуры зуборезного инструмента значения q стандартизованы: 8; 10; 12,5; 16; 20... расчетный шаг червяка: P = π m, ход витка:  Ph = P z1, где: z1 – число витков червяка: 1, 2 или 4 (z1= 3 стандартом не предусмотрено); угол профиля α: для эвольвентных, архимедовых и конволютных червяков α = 20°; диаметр вершин витков: dα1 = d1 + 2m, диаметр впадин витков: df1 = d1 – 2,4m,
делительный угол подъема линии витка (см. рис. 5): tg γ1 = Ph/(π d1) = π m z1/(π m q) = z1/q, длина нарезанной части: –b1. Для червяка в передаче со смещением дополнительно вычисляют: диаметр начального цилиндра (начальный диаметр): dw1 = m/(q + 2x), где х – коэффициент смещения. угол подъема линии витка на начальном цилиндре: tg γ1 = z1/(q + 2x), где х – коэффициент смещения. Межосевое расстояние червячной передачи: a = 0,5(d1 + d2) = 0,5(mq + mz2) = 0,5m(q + z2). Диаметр вершин зубьев(рис. 6): da2 = d2 + 2m(1+x), Диаметр впадин зубьев: df2 = d2 – 2m(1,2 – x), Наибольший диаметр червячного колеса: dam2 ≤ da2 + 6m(z1 +k), Ширина b2 венца червячного колеса зависит от числа витков червяка: b2 = 0,355awпри z1 = 1 или 2 Расчет на прочность: Расчет червячной передачи по контактным напряжениям σн = (170q/z2)×√{KHТ2[(1 +z2/q)/aw]3} ≤ [σн]. Расчет червячной передачи по напряжениям изгиба σF = 0,7YF2(Ft2KF/b2m) ≤ [σF], где КF – коэффициент нагрузки, YF – коэффициент формы зуба, который выбирается из справочных таблиц по приведенному числу зубьев zv2 = z2/cos γ.
Вопрос №26 Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси. Планетарные передачи имеют ряд преимуществ перед обычными: · большие передаточные отношения при малых габаритах и массе · возможность сложения или разложения механической мощности; · лёгкое управление и регулирование скорости; · малый шум вследствие замыкания сил в механизме Недостатки: · Повышенные требования к точности изготовления и монтажа передачи · Резкое снижение КПД передачи с ростом передаточного отношения. Наиболее широкое применение принцип нашёл в планетарных редукторах, автомобильных дифференциалах. На этом принципе работают многие автоматические коробки передач. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1345. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
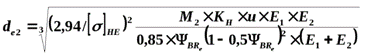 ,
,