
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Классификация зубчатых передачЗубчатые передачи классифицируются по ряду конструктивных признаков и особенностей. В зависимости от взаимного расположения осей, на которых размещены зубчатые колеса, различают передачи цилиндрические (при параллельных осях), конические (при пересекающихся осях) и винтовые (при перекрещивающихся осях). Винтовые зубчатые передачи применяются ограниченно, поскольку имеют низкий КПД из-за повышенного скольжения в зацеплении и низкую нагрузочную способность. Тем не менее, они имеют и некоторые достоинства – высокую плавность хода и возможность выводить концы валов за пределы передачи в обе стороны. На рисунке 1 представлены наиболее широко применяемые виды зубчатых передач:
1 - цилиндрическая прямозубая передача; 2 - цилиндрическая косозубая передача; 3 - шевронная передача; 4 - реечная передача; 5 - цилиндрическая передача с внутренним зацеплением; 6 - винтовая передача; 7 - коническая прямозубая передача; 8 - коническая косозубая передача; 9 - коническая передача со спиралевидными зубьями; 10 - гипоидная передача. В зависимости от вида передаваемого движения различают зубчатые передачи, не преобразующие передаваемый вид движения и преобразующие передаваемый вид движения. К последним относятся реечные зубчатые передачи, в которых вращательное движение преобразуется в поступательное или наоборот. В таких передачах рейку можно рассматривать, как зубчатое колесо с бесконечно большим диаметром. Среди перечисленных видов зубчатых передач наиболее распространены цилиндрические передачи, поскольку они наиболее просты в изготовлении и эксплуатации, надежны и имеют небольшие габариты.  В зависимости от расположения зубьев на ободе колес различают передачи прямозубые, косозубые, шевронные и с круговыми (спиральными) зубьями. Шевронные зубчатые колеса можно условно сравнивать со спаренными косозубыми колесами, имеющими противоположный угол наклона зубьев. Такая конструкция позволяет избежать осевых усилий на валы и подшипники опор, неизбежно появляющихся в обычных косозубых передачах. В зависимости от формы профиля зубьев различают эвольвентные зубчатые передачи и передачи с зацеплением Новикова. Эвольвентное зацепление в зубчатых передачах, предложенное еще в 1760 году российским ученым Леонардом Эйлером, имеет наиболее широкое распространение. В 1954 году в России М. Л. Новиков предложил принципиально новый тип зацеплений в зубчатых колесах, при котором профиль зуба очерчен дугами окружностей. Такое зацепление возможно лишь для косых зубьев. В принципе, возможно изготовление зубчатых передач и с другими формами зубьев – даже квадратными, треугольными или трапецеидальными. Но такие передачи имеют ряд существенных недостатков (непостоянство передаточного отношения, низкий КПД и т. д.), поэтому распространения не получили. В приборах и часовых механизмах иногда встречаются зубчатые передачи с циклоидальным зацеплением. В зависимости от взаимного положения зубчатых колес передачи бывают с внешним и внутренним зацеплением. Наиболее распространены передачи с внешним зацеплением. В зависимости от конструктивного исполненияразличают закрытые и открытые зубчатые передачи. В закрытых передачах колеса помещены в пыле- и влагонепроницаемые корпуса (картеры) и работают в масляных ваннах (зубчатое колесо погружают в масло до 1/3 радиуса). В открытых передачах зубья колес работают всухую или при периодическом смазывании консистентной смазкой и не защищены от вредного воздействия внешней среды. В зависимости от числа ступеней зубчатые передачи бывают одно- и многоступенчатые. В зависимости от относительного характера движения осей зубчатых колес различают рядовые передачи, у которых оси неподвижны, и планетарные зубчатые передачи, у которых ось сателлита вращается относительно центральных осей. *** 21) напряжения действующие на зубья при передаче крутящего момента: При циклических нагрузках допускаемые напряжения зависят от материала и термообработки и также от числа циклов нагружения (времени работы). При постоянном режиме нагрузки:
При переменном режиме нагрузки:
усталостный изгиб: Опасным нагружением считается такое, которое соответствует моменту начала входа зуба в зацепление. Интенсивность нагрузки q p создает две составляющие, из которых одна сжимает, а другая нагибает зуб.
Напряжения изгиба: Допускаемые напряжения определяются как часть от предела усталости (выносливости) материала при симметричном цикле нагружения
22) Прямозубые цилиндрические шестерни Нормальная сила, действующая по линии зацепления, разлагается на две составляющие силы:
На валы действуют те же силы, что и на зубья шестерен, и, кроме того, еще крутящий момент:
23)Особенности расчета косозубых и шевронных Геометрические параметры. У косозубых колес зубья располагаются не по образующей делительного цилиндра, а составляют с ней некоторый угол В торцовом сечении t — t параметры косого зуба изменяются в зависимости от угла Р: окружной шаг pt=pn/cos б) Индексы п и t приписывают параметрам в нормальном и торцовом сечениях соответственно.
П Расчет конической передачи Выбор материала зубчатых колес
С учетом фактических условий нагружения:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 635. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Nц = 60nt – число циклов нагружения
Nц = 60nt – число циклов нагружения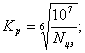

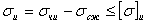
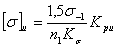 для нереверсивных передач
для нереверсивных передач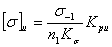 для реверсивных передач
для реверсивных передач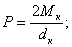
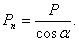
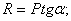
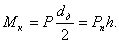
 β (рис. 4.15, где а — косозубая передача; б — шевронная, и рис. 4.16). Оси колес при этом остаются параллельными. Для нарезания косых зубьев используют инструмент такого же исходного контура, как и для нарезания прямых. Поэтому профиль косого зуба в нормальном сечении п—п совпадает с профилем прямого зуба. Модуль в этом сечении должен быть также стандартным .
β (рис. 4.15, где а — косозубая передача; б — шевронная, и рис. 4.16). Оси колес при этом остаются параллельными. Для нарезания косых зубьев используют инструмент такого же исходного контура, как и для нарезания прямых. Поэтому профиль косого зуба в нормальном сечении п—п совпадает с профилем прямого зуба. Модуль в этом сечении должен быть также стандартным .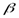 ,окружной модуль mt=mn/cosβ, делительный диаметр d=mtz=mnz/cosβ.
,окружной модуль mt=mn/cosβ, делительный диаметр d=mtz=mnz/cosβ.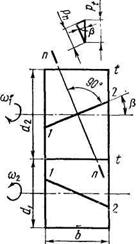
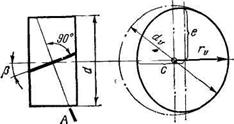 рочность зуба определяют его размеры и форма в нормальномсечении. Форму косого зуба внормальном сечении принято определять через параметры эквивалентного прямозубого колеса(Рис.4.16). Нормальное к зубу сечение образует эллипс с полуосями с=г и e=r/cos β, где r=d/2. В зацеплении участвуют зубья, расположенные на малой оси эллипса, так как второе колесо находится нарасстоянии c—dl2. Радиус кривизны эллипса на малой оси. В соответствии с этим форма косого зуба в нормальном сечении определяется эквивалентным прямозубым колесом, диаметр которого
рочность зуба определяют его размеры и форма в нормальномсечении. Форму косого зуба внормальном сечении принято определять через параметры эквивалентного прямозубого колеса(Рис.4.16). Нормальное к зубу сечение образует эллипс с полуосями с=г и e=r/cos β, где r=d/2. В зацеплении участвуют зубья, расположенные на малой оси эллипса, так как второе колесо находится нарасстоянии c—dl2. Радиус кривизны эллипса на малой оси. В соответствии с этим форма косого зуба в нормальном сечении определяется эквивалентным прямозубым колесом, диаметр которого 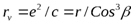 .
.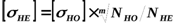 ;
; 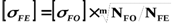 ,
,