
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методи чисельного рішення звичайних диференційних рівнянь при моделюванні електронних схемМета роботи - вивчення методів чисельного розв’язання звичайних диференційних рівнянь при моделюванні електронних схем з LC‑елементами.
Теоретичні відомості
Електронні схеми з реактивними елементами, у загальному випадку, описуються системами звичайних диференційних рівнянь (ЗДР), котрі можуть бути записані у явній
або у неявній формі
Для чисельного розв’язання ЗДР звичайно застосовують формули, що визначають значення функції Un+1 на (n+l)-ому кроці через лінійну комбінацію значень функції та її похідних на попередніх кроках. Число значень функції, що враховуються у формулі, визначає порядок і точність метода. Якщо у формулі використовується значення похідної на (n+l)-ому кроці, то метод зветься неявним, у протилежному випадку - явним. Методи поділяються на абсолютно стійкі, у яких відсутні обмеження на величину кроку, та обмежено стійкі, які мають обмеження на величину кроку. Для аналізу схем широке застосування знаходять наступні найпростіші методи: – явний метод Ейлера:
– неявний метод Ейлера:
– метод трапецій: Тут Формули (4.2б), (4.2в) є абсолютно стійкими. Формула (4.2а) має обмеження на величину кроку:  де lmах - максимальне власне число матриці системи рівнянь. Формули (4.2а) і (4.2б) мають перший порядок, а (4.2в) - другий порядок точності. При однакових умовах застосування формули (4.2а) і (4.2б) дають рівні за величиною і протилежні за знаком похибки апроксимації. Для оцінки похибки апроксимації можна використовувати правило Рунге:
де Un+1(h), Un+1(h/2) - значення функції, отримані в точці При складанні математичної моделі схеми з LC-елементами та її аналізі можливі два способи. За першим способом на підставі диференційних співвідношень для LC-елементів складаються рівняння (4.1а) або (4.1б), що описують схему, а далі за формулами (4.2), або подібними до них, робиться алгебраїзація і розв’язування цих рівнянь. Другий способ передбачає попереднє перетворення за формулами (4.2) диференційних співвідношень для LC-елементів у алгебраїчні з подальшим складанням та розв’язуванням математичної моделі схеми у вигляді системи алгебраїчних рівнянь.
Лабораторне завдання Відповідно до варіанту (див.табл.4.1) скласти програму для розрахунку перехідної характеристики заданої схеми. Схеми приведені на рис. 4.1 - 4.4 Вважати, що вхідним сигналом є ступінчаста функція, рівна нулю при t<0 і Е - при t³0. Початкове значення напруги на С або струму у L рівні нулю. Програма повинна забезпечувати знаходження точного (аналітичного) і чисельного (наближеного) розв’язків ЗДР різними методами, а також обчислення похибки наближених розрахунків, визначеної як різниця між точним і наближеним розв’язками.
Рисунок 4.1 Рисунок 4.2
Рисунок 4.3 Рисунок 4.4
Таблиця 4.1
Точне рішення ЗДР, що описують схеми, має наступний вигляд: – для схеми на рис.4.1 і 4.4:
– для схеми на рис.4.2 і 4.3:
Тут t - постійна часу схеми. Для схем на рис. 4.1 і 4.2 - Для дослідження чисельних методів рішення ЗДР пропонується використовувати наступні рівняння: – для схеми на рис. 4.1:
– для схеми на рис. 4.2:
– для схеми на рис. 4.3:
– для схеми на рис. 4.4:
Для алгебраїзації ЗДР у (4.6) слід використовувати явний і неявний методи Ейлера. При використанні явного методу Ейлера для рівнянь (4.6) отримаємо наступні різністні рівняння: – для схем на рис. 4.1 і 4.2:
– для схем на рис. 4.3 і 4.4:
Обмеження на величину кроку:
При використанні неявного методу Ейлера для рівнянь (4.6) отримаємо наступні різністні рівняння: – для схем на рис. 4.1 і 4.2:
– для схем на рис. 4.3 і 4.4:
Завдання 1. Використовуючи рівняння (4.7) скласти програми для розрахунку перехідних характеристик відповідних схем згідно з варіантом із таблиці 4.1. Розрахунок проводити з постійним кроком h для трьох випадків: h=0.5t, h=2t, h=2.5t. Результати розрахунків представити у вигляді таблиць і графіків. У таблицях для кожного метода і величини кроку h привести значення часу, результати точного і наближеного рішень, а також похибку обчислень. Графічно представити точний за формулами (4.5) і наближений рішення. Завдання 2. Дослідити чисельні методи рішення ЗДР на стійкість і точність. Точність оцінити за правилом Рунге (4.4). Результати оформити у вигляді таблиць Завдання 3. Знайти рішення диференціального рівняння за допомогою функції rkfixed. Примірник програми з використанням функції rkfixed.
Рисунок 4.5
Зміст звіту
1. Формулювання мети досліджень. 2. Еквівалентні схеми і співвідношення, покладені в основу програм. 3. Результати чисельних розрахунків. 4. Дослідження чисельних методів розв’язку ЗДР на стійкість і точність. Точність оцінити за правилом Рунге (4.4). Результати оформити у вигляді таблиць. 5. Вирішення диференціального рівняння за допомогою функції rkfixed. 6. Короткі висновки по результатах досліджень.
Лабораторна робота №8 Моделювання електронних схем з використанням дискретних моделей LC‑елементів Мета роботи - вивчення методів складання дискретних моделей LC‑елементів та їх використання при моделюванні електронних схем.
Теоретичні відомості
При моделюванні схем з LC-елементами у часовій області часто використовується метод, якій передбачає попереднє перетворення диференційних співвідношень для LC-елементів у алгебраїчні з подальшим складанням та розв’язуванням математичної моделі схеми у вигляді системи алгебраїчних рівнянь. Перетворення робиться на підставі неявних методів чисельного рішення ЗДР і здійснює перехід від рівнянь до формул наступного вигляду: – для неявного методу Ейлера (4.8a): UCn+1 = UCn + h/C iCn+1; iLn+1 = iLn + h/L ULn+1. (4.8a)
– для методу трапецій (4.8б): UCn+1 = UCn + 0.5h/C (iCn+ iCn+1); iLn+1 = iLn + 0.5h/L (ULn + ULn+l). (4.8б)
Формули (4.8) прийнято називати дискретними моделями реактивних елементів. За цими моделями можна скласти дискретні схеми заміщення. На рис.4.6, 4.7 наведено дискретні схеми заміщення LC-елементів, які побудовані за співвідношеннями (4.8) (а - реактивний елемент, б - послідовна, в - паралельна схеми заміщення). Параметри компонентів схем заміщення наведено у табл. 4.2 для ємності і у табл.4.3 - для індуктивності.
Таблиця 4.2
Таблиця 4.3
Рисунок 4.6 – Дискретні схеми заміщення ємності
Рисунок 4.7 – Дискретні схеми заміщення індуктивності
Слід відзначити, що використання дискретних схем заміщення дозволяє перетворити реактивні схеми з реактивними елементами у резистивні схеми, а аналіз у часовій області замінити послідовністю розрахунків еквівалентної резистивної схеми за постійним струмом.
При заміні ємності у схемі на рис. 4.1 дискретною схемою заміщення послідовного типу (рис. 4.6б) і скориставшись 2-м законом Кірхгофа отримаємо наступне рівняння кола
Після підстановки в це рівняння співвідношення із (4.8а) у формі
і здійснення простих перетворень отримаємо кінцеве ітераційне рівняння відносно напруги на ємності С
Вихідною напругою даної схеми є напруга на резисторі R, яка обчислюється за формулою
Аналогічно, якщо виконати заміну індуктивності у схемі на рис. 4.3 дискретною схемою заміщення 4.7б, то за 2-м законом Кірхгофа отримаємо рівняння
Підстановка співвідношення із (4.8а) у вигляді
дає кінцеву форму ітераційного рівняння для струму через індуктивність
Для вихідної напруги на резисторі R будемо мати
Лабораторне завдання
Згідно з варіантом із таблиці 4.1 виконати розрахунок схеми, обравши дискретну схему заміщення реактивного елемента (див. рис.4.6, 4.7 і таблиці 4.2, 4.3), відповідну до неявного методу Ейлерата метода трапецій. Складіть моделі схеми, що аналізується, у вигляді резистивного кола. За законами Кірхгофа запишіть рівняння кола і отримайте співвідношення для струмів і напруг у (n+1)-й момент часу. Організуйте цикл за часом з кроком h і перевизначте після кожного кроку незалежні джерела у дискретних схемах заміщення. Зміст звіту
1 Формулювання мети досліджень. 2. Еквівалентні схеми і співвідношення, покладені в основу програм. 3. Программа знаходження вихідної напруги з використанням дискретних моделей LC‑елементів та неявного методу Ейлера. Результати чисельних розрахунків у вигляді таблиці і графіка залежності віхідної напруги від часу. 4. Программа знаходження вихідної напруги з використанням дискретних моделей LC‑елементів та методу трапеції. Результати чисельних розрахунків у вигляді таблиці і графіка залежності віхідної напруги від часу. 5. Порівняти отримані результати . 5. Короткі висновки по результатах досліджень.
Контрольні запитання
1. Запишіть диференційні співвідношення для струму і напруги у LC-елементах. 2. Вкажіть дві форми подання систем ЗДР. 3. Дайте класифікацію методів чисельного рішення ЗДР. 4. Запишіть явну і неявну формули Ейлера, дайте пояснення. 5. Запишіть формулу трапецій, дайте пояснення. 6. Вкажіть різницю явних методів і неявних. 7. Яке обмеження на крок має явний метод Ейлера? 8. Як оцінити похибку обчислень за правилом Рунге?
5 ОПТИМІЗАЦІЯ ЕЛЕКТРОННИХ СХЕМ Теоретичні відомості Під оптимізацією електронної схеми розуміється цілеспрямований|ціленаправлений| пошук оптимальних значень параметрів елементів схеми, при яких її характеристики найкращим чином задовольняють поставленим в технічному|технічний| завданні|задавання| вимогам. При цьому структура схеми задається розробником, а вибір значень параметрів елементів проводиться|виробляється,справляється| за допомогою ЕОМ за програмами, що реалізують методи рішення задач нелінійного|нелінійний| програмування. У загальному|спільний| випадку завдання|задача| нелінійного|нелінійний| програмування формулюється таким чином: знайти мінімум|мінімум-ареал| функції F(x) при обмеженнях: типу|тип| рівності (5.1) типу|тип| нерівностей Функція F(x) називається цільовою|цільовий| функцією. Якщо цільова|цільовий| функція і обмеження є|з'являтися,являтися| лінійними функціями, то має місце завдання|задача| лінійного програмування, при квадратичній цільовій|цільовий| функції і лінійних обмеженнях – завдання|задача| квадратичного програмування, і, нарешті|урешті|, у разі|в разі| відсутності|відсутність| обмежень – завдання|задача| безумовної мінімізації. Для постановки і рішення оптимізаційної задачі необхідно скласти цільову|цільовий| функцію, за допомогою якої оцінюється ступінь|міра| відповідності характеристики схеми, що оптимізується, технічному|технічний| завданню|задавання|. На практиці широке|широкий| застосування|вживання| отримали|одержали| цільові|цільовий| функції, складені по середньостепеневому|середньоквадратичний| критерію оптимальності:
де m –| число крапок|точка,точка-тире|, на яке розбивається інтервал зміни змінній w (частоти, часу і т.п.), в якому проводиться|виробляється,справляється| оптимізація характеристики;
P- ступінь|міра| наближення. При рівноцінності всіх точок характеристики можна покласти
Зі|із| збільшенням Мінімальне значення ступеня|міра| наближень p дорівнює 2. Зі збільшенням ступеня|міра| p відбувається|походити| вирівнювання помилок|помилка| У окрузі|околиця| шуканої точки мінімуму|мінімум-ареал|
де
матриця Гессе (матриця других приватних похідних); t - знак транспонування.
Якщо Остання умова означає позитивну визначеність матриці|матриця| Гессе. Квадратичну функцію (7.3) можна записати таким чином:
де а - постійна; Н - квадратна позитивно визначена матриця. Ефективність методів оптимізації визначається швидкістю знаходження мінімуму|мінімум-ареал| квадратичних функцій (5.4). Якщо мінімум (5.4) знаходиться|перебувати| за n кроків, то використовуваний метод мінімізації має квадратичну збіжністю. Найповніше розроблені математичні методи рішення задачі безумовної мінімізації. Більшість з|із| них засновані на побудові|шикування| ітераційного процесу пошуку мінімуму|мінімум-ареал|, що здійснює перетворення завдання|задача| знаходження мінімуму|мінімум-ареал| функції
яка описує переміщення з|із| кроком α із початкової точки У простому випадку одновимірний|одномірний| пошук можна здійснити шляхом послідовного збільшення кроку Ефективність ітераційного алгоритму безумовної мінімізації визначається способом побудови|шикування| напрямів|направлення| пошуку При побудові|шикування|
До методів другого порядку|лад| відноситься метод Ньютона, формулу якого можна отримати|одержати|, якщо розкладання (5.3) цільової|цільовий| функції в ряд|лава,низка| провести|виробити,справити| в крапці
Звідси витікає формула даного методу:
де У разі|в разі| квадратичної функції формула (5.6) при будь-якій початковій точці
Для функції двох змінних формулу (5.7) можна перетворити до вигляду|вид|:
де
Лабораторна робота №9 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 324. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 , (4.1а)
, (4.1а) . (4.1б)
. (4.1б) (4.2a)
(4.2a) (4.2б)
(4.2б)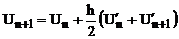 (4.2в)
(4.2в) - крок за часом;
- крок за часом;  ,
,  - похідні у точках
- похідні у точках  та
та  відповідно.
відповідно. , (4.3)
, (4.3)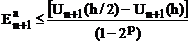 , (4.4)
, (4.4) при переході з точки
при переході з точки  з кроком h і з кроком h/2, відповідно; p - порядок точності методу.
з кроком h і з кроком h/2, відповідно; p - порядок точності методу.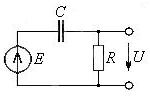



 , (4.5а)
, (4.5а) . (4.5б)
. (4.5б) , для схем на рис.4.3 і 4.4 -
, для схем на рис.4.3 і 4.4 -  .
. ,
,  , (4.6а)
, (4.6а) , (4.6б)
, (4.6б) ,
,  , (4.6в)
, (4.6в) ,
,  . (4.6г)
. (4.6г) , (4.7а)
, (4.7а) . (4.7б)
. (4.7б) .
.  , (4.7в)
, (4.7в) . (4.7г)
. (4.7г)

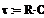
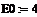






 ,
,


 .
.
 .
. .
. .
.
 .
. .
. , і = 1,2,...,k;
, і = 1,2,...,k; >= 0, і =1,2,…,m
>= 0, і =1,2,…,m (5.2)
(5.2) - ваговий коефіцієнт для крапки|точка,точка-тире|
- ваговий коефіцієнт для крапки|точка,точка-тире|  ;
; - необхідне значення характеристики у і–й крапці;
- необхідне значення характеристики у і–й крапці; - реалізоване значення характеристики у і–й крапці.
- реалізоване значення характеристики у і–й крапці.  ,
, 
 внесок|вклад| і-й крапки|точка,точка-тире| в цільову|цільовий| функцію збільшується, що веде до точнішого виконання вимог для значень характеристики в цій крапці|точка,точка-тире|.
внесок|вклад| і-й крапки|точка,точка-тире| в цільову|цільовий| функцію збільшується, що веде до точнішого виконання вимог для значень характеристики в цій крапці|точка,точка-тире|. і характеристика, що оптимізується, наближається формою до рівноволнової.
і характеристика, що оптимізується, наближається формою до рівноволнової. довільну цільову|цільовий| функцію
довільну цільову|цільовий| функцію  від n змінних можна апроксимувати квадратичною функцією, використавши розкладання
від n змінних можна апроксимувати квадратичною функцією, використавши розкладання  (5.3)
(5.3) ;
; - градієнт цільової|цільовий| функції;
- градієнт цільової|цільовий| функції;
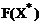 є|з'являтися,являтися| мінімумом|мінімум-ареал|, то при будь-якому малому прирості ΔХ функция
є|з'являтися,являтися| мінімумом|мінімум-ареал|, то при будь-якому малому прирості ΔХ функция 
 .
. , (5.4)
, (5.4) - транспонований вектор n змінних;
- транспонований вектор n змінних; , (5.5)
, (5.5) в точку|точка,точка-тире|
в точку|точка,точка-тире|  у напрямі|направлення| на мінімум|мінімум-ареал|, вектором, що задається
у напрямі|направлення| на мінімум|мінімум-ареал|, вектором, що задається  . Таким чином, на к-й| ітерації ставиться завдання|задача| знаходження оптимального значення кроку, що мінімізує цільову|цільовий| функцію
. Таким чином, на к-й| ітерації ставиться завдання|задача| знаходження оптимального значення кроку, що мінімізує цільову|цільовий| функцію  в напрямі|направлення|
в напрямі|направлення|  на величину h. При кожному збільшенні слід проводити|виробляти,справляти| порівняння поточного
на величину h. При кожному збільшенні слід проводити|виробляти,справляти| порівняння поточного  ,
,  і попереднього,
і попереднього,  ,
,  значень цільової|цільовий| функції. Якщо
значень цільової|цільовий| функції. Якщо  <
<  (вдалий|успішний| крок), то до
(вдалий|успішний| крок), то до  знов|знову,щойно| додається|добавляється| h.. Інакше поточна невдала крапка|точка,точка-тире| відкидається, h зменшується, наприклад, удвічі,|вдвічі| і повторюється пошук мінімуму|мінімум-ареал| з|із| зменшеним h |із|їз попередньої вдалої|успішний| крапки|точка,точка-тире|
знов|знову,щойно| додається|добавляється| h.. Інакше поточна невдала крапка|точка,точка-тире| відкидається, h зменшується, наприклад, удвічі,|вдвічі| і повторюється пошук мінімуму|мінімум-ареал| з|із| зменшеним h |із|їз попередньої вдалої|успішний| крапки|точка,точка-тире|  . Точність знаходження мінімуму|мінімум-ареал| визначається величиною h.
. Точність знаходження мінімуму|мінімум-ареал| визначається величиною h. , а в методах другого порядку|лад| – матриця Гессе
, а в методах другого порядку|лад| – матриця Гессе  .
. , а функцію
, а функцію  . Потім знайти градієнт цільової|цільовий| функції
. Потім знайти градієнт цільової|цільовий| функції  в крапці|точка,точка-тире|
в крапці|точка,точка-тире|  .
. , (5.6)
, (5.6) - матриця, зворотна матриці|матриця| Гессе.
- матриця, зворотна матриці|матриця| Гессе. . При мінімізації довільної функції ітерації будуються по формулі (5.5) з|із| напрямами:|направлення|
. При мінімізації довільної функції ітерації будуються по формулі (5.5) з|із| напрямами:|направлення| . (5.7)
. (5.7) , (5.8)
, (5.8) - визначник матриці|матриця| Гессе.
- визначник матриці|матриця| Гессе.