
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Аналіз математичної моделі електронної схемиМета|ціль| роботи- освоєння|основний| методів рішення|розв'язання,вирішення,розв'язування| систем лінійних алгебраїчних рівнянь при аналізі лінійних електронних схем.
Теоретичні відомості Математична модель схеми, що складена по методу вузлових потенціалів, описується співвідношенням (2.7), яке є системою лінійних алгебраїчних рівнянь, записаною в матричній формі|форма|. Рішення систем лінійних алгебраїчних рівнянь вида
може бути виконано прямими і ітераційними методами. Прямі методи дозволяють безпосередньо отримувати|одержувати| рішення|розв'язання,вирішення,розв'язування| систем рівнянь. Ітераційні методи засновані на побудові|шикування| послідовних наближень, що сходяться до рішення, що треба знайти|розв'язання,вирішення,розв'язування|. Для вирішення завдань|задача| схемотехніки в системах автоматизованого проектування використовуються прямі методи, такі як метод Гауса|Гаус| і метод LU-розкладання. Метод Гауса|Гаус| ґрунтується на послідовному виключенні|виняток| невідомих, що складають вектор Х в (2.12). Під час прямого ходу методу Гауса|Гаус| квадратна матриця А матричного рівняння (2.12) в результаті|унаслідок,внаслідок| послідовного виключення|виняток| невідомих|із| розкладається| на дві трикутні|трикутний| матриці|матриця|: нижню трикутну|трикутний| (L-матрицю|матриця|) і верхню трикутну|трикутний| (U-матрицю|матриця|). Під час зворотного ходу методу Гауса|Гаус| здійснюється рішення|розв'язання,вирішення,розв'язування| системи рівнянь з|із| верхньою трикутною матрицею|матриця|. На рішення|розв'язання,вирішення,розв'язування| системи з|із| n рівнянь методом Гауса|Гаус| потрібно 
довгих операцій (множення і ділення|поділка,розподіл,поділ|). Метод LU-розкладання, заснований на представленні матриці|матриця| А в матричному рівнянні (2.12) у вигляді перемноження|добуток| нижньої| і верхньої трикутних|трикутний| матриць|матриця|
На підставі цього розкладання матричне рівняння (2.12) перетвориться в два рівняння:
Рішення|розв'язання,вирішення,розв'язування| проводиться в два етапи. На першому|перший| етапі з|із| рівняння (2.15) по заданому вектору В знаходиться|перебувати| вектор допоміжних змінних Y. На другому етапі по знайденому Y розраховується шуканий вектор X. Основну|основний| кількість довгих операцій ( У MATHCADе| рішення|розв'язання,вирішення,розв'язування| систем рівнянь (2.12) можна здійснити різними способами. За допомогою функції lsolve| рішення|розв'язання,вирішення,розв'язування| систем лінійних рівнянь алгебри:
Методом зворотної матриці|матриця|, використовуючи оператор обертання|звертання,обіг| матриці|матриця| «-1»:
Методом LU-розкладання за допомогою функції lu|. Результатом роботи цієї функції буде прямокутна матриця, що складається з трьох квадратних матриць|матриця|: матриці|матриця| перенумерації| P, нижньої трикутної матриці|матриця| L, верхньої трикутної| матриці|матриця| U. Якщо Р діагональна матриця, то нумерація клітин|клітина| матриць|матриця| не міняється. Для виділення підматриць|матриця| з|із| матриці|матриця| R використовується функція submatrix|. Наприклад, програму LU-розкладання матриці| А розмірністю
Лабораторне завдання
За даними лабораторної роботи №3 провести аналіз схеми на рис. 2.1, використовуючи математичну модель (2.7), складену по методу вузлових потенціалів. Аналіз здійснити на частоті 1. Рішення|розв'язання,вирішення,розв'язування| матричного рівняння (2.7) виконати різними способами: - за допомогою функції lsolve| рішення|розв'язання,вирішення,розв'язування| систем лінійних рівнянь алгебри; - методом LU-розкладання; - за допомогою зворотної матриці|матриця|. 2. По співвідношеннях (2.3) – (2.5) знайти напругу|напруження| і струми|тік| на елементах схеми. 3. Обчислити|обчисляти,вичислити| коефіцієнт передачі|передача| схеми по струму|тік|
де J1 – струм|тік| на вході схеми, 4 Обчислити|обчисляти,вичислити| коефіцієнт передачі|передача| схеми по напрузі
де
Зміст|вміст,утримання| звіту 1. Короткі теоретичні відомості, розрахункові формули, досліджувані схеми. 2. Значення елементів|роздруківка,роздрукування| матриці|матриця| 3. Значення елементів|роздруківка,роздрукування| векторів
6. Короткі висновки|висновок,виведення| по роботі.
Контрольні питання
1. У чому суть прямого і зворотного ходу методу Гауса|Гаус|? Перерахуєте його достоїнства і недоліки|нестача,недолік|? 2. Кількість довгих операцій в методі Гауса|Гаус|. 3. Пояснить алгоритм методу LU-розкладання. Достоїнства і недоліки|нестача,недолік| цього методу. 4. Пояснить операцію факторизації матриці|матриця|. 5. Як визначаються коефіцієнти передачі|передача| схеми по струму|тік| і напрузі|напруження|? 6. Область застосування|вживання| функції lsolve|,її вхідні і вихідні змінні. 7. Скласти і пояснити програму рішення|розв'язання,вирішення,розв'язування| систем лінійних рівнянь алгебри за допомогою функції lu|. 8. Пояснить метод зворотної матриці|матриця|. Скласти програму його використання. 9. Як розраховується вектор струмів 10. Як розраховуються векторі напруг
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 296. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
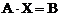 (2.12)
(2.12)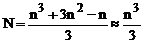 (2.13)
(2.13)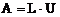 . (2.14)
. (2.14)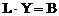 , (2.15)
, (2.15)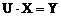 . (2.16)
. (2.16)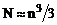 ) складає факторизація матриці|матриця| А, тобто розкладання (2.14). Рішення|розв'язання,вирішення,розв'язування| рівнянь (2.15), (2.16) з|із| трикутними|трикутний| матрицями|матриця| вимагає мінімальне число операцій (
) складає факторизація матриці|матриця| А, тобто розкладання (2.14). Рішення|розв'язання,вирішення,розв'язування| рівнянь (2.15), (2.16) з|із| трикутними|трикутний| матрицями|матриця| вимагає мінімальне число операцій ( 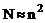 ). Перевага|чеснота,достоїнство| цього методу полягає в тому, що виконавши один раз факторизацію матриці|матриця| А, можна потім вирішувати|рішати,розв'язати| рівняння (2.12) для різних векторів В.
). Перевага|чеснота,достоїнство| цього методу полягає в тому, що виконавши один раз факторизацію матриці|матриця| А, можна потім вирішувати|рішати,розв'язати| рівняння (2.12) для різних векторів В.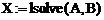 .
.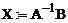 .
.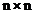 з|із| подальшим|наступний| розв'язанням|розв'язання,вирішення,розв'язування| рівняння (2.12), можна записати у вигляді|вид|:
з|із| подальшим|наступний| розв'язанням|розв'язання,вирішення,розв'язування| рівняння (2.12), можна записати у вигляді|вид|: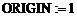
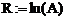
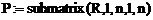
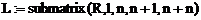
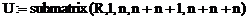
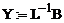
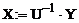
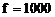 Гц.
Гц.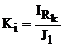 ,
,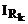 - струм|тік| в резисторі Rk.
- струм|тік| в резисторі Rk.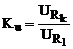 ,
,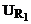 – напруга|напруження| на вході схеми,
– напруга|напруження| на вході схеми, 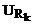 - напруга|напруження| на резисторі Rk.
- напруга|напруження| на резисторі Rk.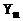 , вектора
, вектора 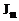 , вектора вузлових потенціалів φ на частоті
, вектора вузлових потенціалів φ на частоті 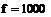 Гц.
Гц.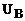 ,
, 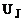 ,
, 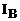 , що відповідають |із| напругам|напруження| і струмам|тік| в елементах схеми.
, що відповідають |із| напругам|напруження| і струмам|тік| в елементах схеми.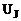 ?
?