Методы вариационного исчисления и теории оптимального управления

Вариационное исчисление – математическая дисциплина, посвященная отысканию экстремальных (наибольших или наименьших) значений функционалов [1]. В свою очередь под функционалом понимается числовая (действительная или комплексная) функция, определенная на некотором множестве функций. Вариационное исчисление является естественным развитием той главы математического анализа, которая посвящена задаче отыскания экстремумов функций. В основе постановки задач классического вариационного исчисления лежат задачи управления физическими процессами. Во всех вариантах таких задач речь идет о способе задания наилучшего в том или другом смысле управления, обеспечивающего минимизацию или максимизацию некой цели управления.

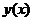В одной из возможных постановок [6] предметом вариационного исчисления является отыскание неизвестных функций  или , реализующих максимум или минимум определенных интегралов вида

или

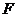где  ‑ функция, описывающая взаимосвязь поведения объекта в зависимости от управления. На функцию  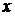накладывается ряд требований, в частности, требования непрерывности производных на интервале определения, что всегда обеспечивается в задачах с физическими процессами и не всегда в задачах экономики и менеджмента. В большинстве приложений функции  или  выбираются не среди множества всех возможных функций от , а среди множества функций определенного класса. Такое допущение оправдано в связи с тем, что возможности управления процессом очень часто ограничивают класс возможных функций неким заранее заданным.

Развитие идей вариационного исчисления привело к определенной модернизации постановки исходной задачи в виде учета ограничений функции  и созданию теории оптимального управления. Методы решения подобных задач опираются на реализацию так называемого принципа максимума Понтрягина [1]. Практическая реализация методов вариационного исчисления и теории оптимального управления позволяет решать динамические задачи разработки управленческого решения.