Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
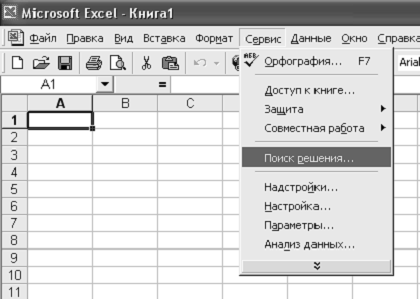
Использование Excel для поиска экстремумов функцийЭлектронные таблицы Excel фирмы Microsoft имеют встроенные средства решения задач поиска экстремума, оформленные в виде так называемой надстройки. Перед началом работы надо убедиться в том, что в составе сгенерированного на вашей ЭВМ пакета Excel требуемая надстройка установлена. Для этого выберите режим Сервис главного меню и проверьте, есть ли в открывшемся ниспадающем меню пункт Поиск решения(рис. 5). Если строка меню Поиск решения отсутствует, то выберите пункт меню Сервис / Надстройки и в открывшейся форме включите режим Поиск решения (рис. 6). Если и в этом окне пункт Поиск решения отсутствует, то это означает, что на вашей машине установлена сокращенная версия электронных таблиц и требуется переустановка пакета Excel. Надстройка Поиск решения (рис. 7) позволяет, задавая некоторую ячейку в виде целевой (Установить целевую ячейку), при условии обеспечения зависимости результата вычислений в ней от значений некоторых изменяемых ячеек (Изменяя ячейки) с учетом заданных ограничений (Ограничения) получить набор переменных в изменяемых ячейках, обеспечивающий или максимальное, или минимальное, или заданное значение целевой ячейки. В качестве параметров режима (рис. 8) задаются методы поиска экстремума. Так, при установке флажка Линейная модель надстройка ищет экстремум симплекс-методом. Флажок Неотрицательные значения накладывает дополнительное ограничение на значения переменных задачи. Его установка эквивалентна введению ограничения Примечание. Если флажок Линейная модель выключен, решение задачи ведется методом Ньютона или градиентным с использованием прямых или центральных конечных разностей на основе линейной или квадратичной оценки уменьшения приращения экстремума в зависимости от установленных флажков. Эти методы позволяют, в частности, решать нелинейные и целочисленные задачи поиска экстремумов. 
Рис. 5. Пункт меню Поиск решения
Рис. 6. Включение надстройки Поиск решения Режим Автоматическое масштабирование позволяет перейти к отображению данных в относительных единицах, а при установке флажка Показывать результаты итераций включается пошаговый режим. Также к числу параметров относится ограничение по времени процесса поиска решения в секундах (Максимальное время) (максимально 32767) и количеству итераций (Предельное число итераций). Вариант настройки параметров режима Поиск решения может быть сохранен. Примечание. Точность соответствия результата заданному значению (Относительная погрешность), допустимого отклонения экстремума от оптимального значения при использовании режима целочисленной математики (Допустимое отклонение), а также условие прекращения поиска экстремума (Сходимость), задающее величину относительного приращения экстремума за последние пять итераций относятся к параметрам, используемым при решении задачи методом Ньютона или градиентным.
Рис. 7. Главная форма надстройки Поиск решения Рассмотрим задачу линейного программирования (1,2), записанную в виде целевой (критериальной) функции и набора ограничений, с конкретными числовыми данными, полученными с помощью датчика случайных чисел.
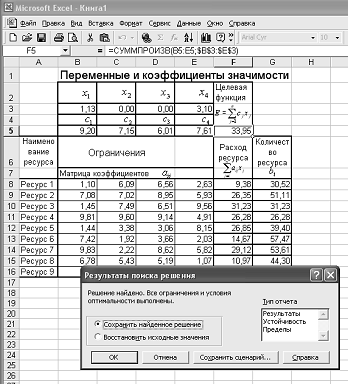
На рис. 9 изображен рабочий лист Excel с данными задачи (4). Для всех ячеек, предназначенных для хранения данных, был задан числовой формат с двумя знаками после запятой режимом Формат/Ячейки…/Число. Матрица
Рис. 8. Параметры надстройки Поиск решения Выражение (3) представляет собой ничто иное, как сумму Выражения, определяющие расход ресурсов Примечание. Остальная информация, нанесенная на рабочий лист (рис. 9), используется для пояснения принципа размещения данных. Она представляет собой либо текстовые строки, записанные в определенные ячейки, либо внедренные объекты и носит вспомогательный характер. Поэтому при повторении примера на ЭВМ она может быть опущена.
Рис. 9. Вариант размещения данных на рабочем листе Выполненные ранее в операции (заполнение таблиц данными и программирование формул) позволяют полностью подготовиться собственно к решению задачи оптимизации. Теперь нам необходимо вызвать режим Сервис/Поиск решения. В открывшейся главной форме меню режима Поиск решения (рис. 7) надо указать адрес нашей целевой ячейки F5 и проверить или задать тип экстремума (в нашем случае Установить целевую ячейку равной максимальному значению). В окне Изменяя ячейки задаем адреса ячеек переменных Нажимаем кнопку Выполнить и получаем решение задачи, показанное на рис. 12. В результате выполнения команды Поиск решения в таблицеРезультаты поиска решениямогут быть выданы следующие диагностические сообщения: Решение найдено. Все ограничения и условия оптимальности выполнены (имеет место в рассматриваемом случае). Поиск не может найти подходящего решения. Значения целевой ячейки не сходятся. Если решение найдено, то на рабочем листе Excel в изменяемых ячейках находятся значения переменных Если в результате решения задачи оптимизации выдается сообщение Поиск не может найти подходящего решения, то это означает, что условия задачи несовместны, т. е. не существует такого набора значений переменных Диагностическое сообщение Значения целевой ячейки не сходятся выдается Excel в том случае, когда при поиске максимума целевой функции область допустимых значений целевой функции не ограничена сверху (целевая функция возрастает неограниченно). Для устранения этой причины целесообразно увеличить количество ограничений на значения переменных.
Рис. 10. Добавление ограничений
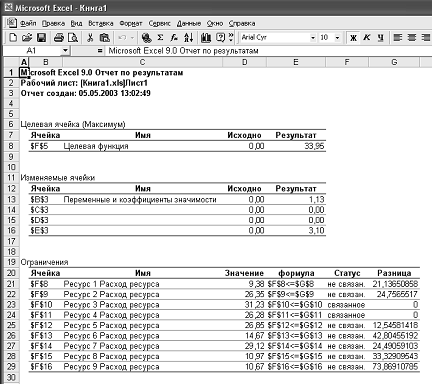
Рис. 11. Подготовленная к решению задача линейного программирования По результатам решения в случае установки режима Линейная модель (симплекс-метод) могут быть представлены три типа отчетов: по результатам, по устойчивости и по пределам. Если они требуются, то в меню результаты поиска решения в окне Тип отчета (рис. 12) необходимо выделить соответствующие строки. Отчет по результатам (рис. 13) содержит начальные (Исходно) и конечные (Результат) значения целевой функции и изменяемых ячеек, а также сводку результатов использования ресурсов. В этой сводке в столбце Статус символами связанное или несвязанное обозначаются соответственно полное или неполное использование соответствующего ресурса. В рассматриваемом примере полностью израсходованы Ресурс 3 и Ресурс 4.
Рис. 12. Результат решения задачи линейного программирования Отчет по устойчивости (рис. 14) показывает значения нормированной стоимости оценок (Нормир. стоимость), определяющих насколько изменится целевая функция при принудительном включении в план единицы продукции. Кроме этого в отчете содержатся величины использованных ресурсов (Результ. значение), их теневые цены, показывающие насколько изменится целевая функция при увеличении соответствующего ресурса на единицу, а также используемые значения ограничений. Колонки Допустимое увеличение (уменьшение) задают диапазон изменения значений переменных и ограничений, сохраняющих общую структуру решения задачи.
Рис. 13. Отчет по результатам
Рис. 14. Отчет по устойчивости Отчет по пределам (рис. 15) показывает возможный диапазон изменения значений переменных, сохраняющий структуру оптимального решения, а также получающиеся в этом случае значения целевой функции. Примечание. Конкретные реализации состава таблиц отчетов по пределам и устойчивости могут отличаться от приведенных выше.
Рис. 15. Отчет по пределам |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 603. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
.


 (4)
(4) размещена в диапазоне ячеек B8:E16. Значения ограничений
размещена в диапазоне ячеек B8:E16. Значения ограничений  находятся в диапазоне ячеек G8:G16. Весовые коэффициенты целевой функции
находятся в диапазоне ячеек G8:G16. Весовые коэффициенты целевой функции 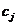 занесены в диапазон ячеек B5:E5. Кроме этого, для хранения переменных
занесены в диапазон ячеек B5:E5. Кроме этого, для хранения переменных  зарезервирован диапазон ячеек B3:E3. Значения
зарезервирован диапазон ячеек B3:E3. Значения  ,
,  .
.
 попарных произведений некоторых наборов чисел, которые должны быть заданы в табличной форме или рассчитаны средствами пакета Excel. Рассчитаем значение целевой функции
попарных произведений некоторых наборов чисел, которые должны быть заданы в табличной форме или рассчитаны средствами пакета Excel. Рассчитаем значение целевой функции  в ячейке F5. Ее программирование сводится к заданию выражения типа (3), которое можно рассчитать непосредственно на основе формулы Excel =B3*B5+C3*C5+D3*D5+E3*E5. Тем не менее, по ряду причин, более удобно воспользоваться встроенной функцией СУММПРОИЗВ(B5:E5;$B$3:$E$3), которая автоматически определяет количество слагаемых
в ячейке F5. Ее программирование сводится к заданию выражения типа (3), которое можно рассчитать непосредственно на основе формулы Excel =B3*B5+C3*C5+D3*D5+E3*E5. Тем не менее, по ряду причин, более удобно воспользоваться встроенной функцией СУММПРОИЗВ(B5:E5;$B$3:$E$3), которая автоматически определяет количество слагаемых  и дает результат вычислений в соответствии с (3). Использование абсолютного формата записи диапазона ячеек, используемого для хранения
и дает результат вычислений в соответствии с (3). Использование абсолютного формата записи диапазона ячеек, используемого для хранения  , не является обязательным, однако удобно для последующих действий, которые могут выполняться способом копирования.
, не является обязательным, однако удобно для последующих действий, которые могут выполняться способом копирования. программируются в ячейки F8, F9,…, F16 аналогично предыдущему с той только разницей, что в качестве первого аргумента функции СУММПРОИЗВ() выступает соответствующая строка матрицы
программируются в ячейки F8, F9,…, F16 аналогично предыдущему с той только разницей, что в качестве первого аргумента функции СУММПРОИЗВ() выступает соответствующая строка матрицы 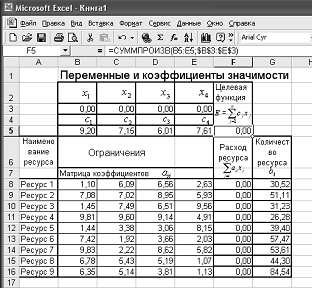
 (в нашем случае B3:F3). Нажав кнопку Добавить в открывшейся таблице (рис. 10) Добавление ограничения в поле Ссылка на ячейку вводим адреса левых частей неравенств (2) (в нашем случае F8:F16). Устанавливаем (сохраняем) требуемые знаки неравенств (в нашем случае
(в нашем случае B3:F3). Нажав кнопку Добавить в открывшейся таблице (рис. 10) Добавление ограничения в поле Ссылка на ячейку вводим адреса левых частей неравенств (2) (в нашем случае F8:F16). Устанавливаем (сохраняем) требуемые знаки неравенств (в нашем случае  ). Войдя в окно Ограничение, задаем адреса ячеек, содержащих значения
). Войдя в окно Ограничение, задаем адреса ячеек, содержащих значения  (в нашем случае G8:G16). Нажав кнопку Параметры, в открывшейся таблице (рис. 8) задаем режим Линейная модель и Неотрицательные значения, после чего нажимаем кнопку OK. Результат этих действий отображен на рис11.
(в нашем случае G8:G16). Нажав кнопку Параметры, в открывшейся таблице (рис. 8) задаем режим Линейная модель и Неотрицательные значения, после чего нажимаем кнопку OK. Результат этих действий отображен на рис11. (в нашем случае 1,13; 0,00; 0,00; 3,10), обеспечивающие максимальное значение целевой функции (в нашем случае 33,95). Для сохранения результатов вычислений на рабочем листе необходимо выбрать пункт Сохранить найденное решение.
(в нашем случае 1,13; 0,00; 0,00; 3,10), обеспечивающие максимальное значение целевой функции (в нашем случае 33,95). Для сохранения результатов вычислений на рабочем листе необходимо выбрать пункт Сохранить найденное решение. , который удовлетворял бы имеющимся ограничениям.
, который удовлетворял бы имеющимся ограничениям.