
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сложение свободных гармонических колебаний
Сложение гармонические колебания одного направления и одинаковой частоты
Тогда уравнение результирующего колебания будет иметь вид
Амплитуда результирующего колебания
Начальная фаза суммарного колебания
Пример 14.10.Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами А0. Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания. А)p/3 В) p С) 0 £А02032А01А0Ö3 Решение: амплитуда результирующего колебания двух гармонических колебаний одного направления с равными амплитудами А0 рассчитывается по формуле
При разности фаз 1) 2) 3)
Сложение взаимно перпендикулярных колебаний с одинаковой частотой
При сложении гармонических колебаний одинаковой частоты ω, происходящих во взаимно перпендикулярных направлениях вдоль осей x и y, для простоты полагают начальную фазу первого колебания φ1=0. Тогда
где α — разность фаз обоих колебаний, А и В ― амплитуды складываемых колебаний. После преобразований получается уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно:
Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз α. Некоторые частные случаи, представляющие физический интерес: 1) α=mπ (m=0, ±1, ±2, …). В данном случае эллипс вырождается в отрезок прямой: 2) α=(2m+1)π/2 (m=0, ±1, ±2, …). В данном случае уравнение примет вид 
Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам. ЕслиА=В, то эллипс вырождается в окружность.
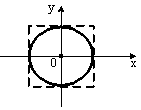
Пример 14.11. Складываются два взаимно перпендикулярных колебания. Установите соответствие между номером соответствующей траектории и законами колебаний точки вдоль осей координат. А) C)
1)A 3)C 5)£ Решение: при одинаковой частоте складываемых колебаний уравнение траектории точки имеет вид: Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам. В ответе №1 α = π/2, а амплитуды исходных колебаний различны, что удовлетворяет форме фигуры А(эллипс). Если амплитуды исходных колебаний одинаковы, то эллипс вырождается в окружность. В ответе №3 α = 3π/2 и амплитуды совпадают, что удовлетворяет форме фигурыС (окружность).
Пример 14.12. Установите соответствие между сопротивлением и его численным значением А. Активное сопротивление
С) Полное сопротивление А40 Ом В30 Ом С50 Ом £20 Ом Решение: Используем метод векторных диаграмм. Длина вектора равна амплитудному значению напряжения, а угол, который вектор составляет с осью ОХ, равен разности фаз колебаний напряжения на соответствующем элементе и колебаний силы тока в цепи. Сложив три вектора, найдем амплитудное значение полного напряжения:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1082. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |






 ,
,  , тогда
, тогда  ;
; ,
,  , тогда
, тогда  ;
; ,
, 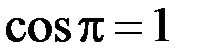 , тогда
, тогда 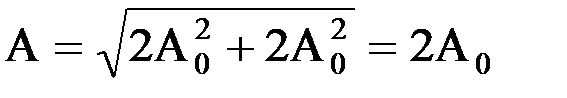 .
.

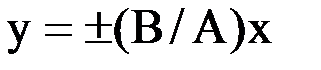 , где знак плюс соответствует нулю и четным значениям m, а знак минус — нечетным значениям m.
, где знак плюс соответствует нулю и четным значениям m, а знак минус — нечетным значениям m.
 B)
B) 
 D)
D) 
 2)B
2)B 
 4)D
4)D 

 Это уравнение эллипса, где α — разность фаз колебаний. Если α=mπ (m=0, ±1, ±2, …), эллипс вырождается в отрезок прямой
Это уравнение эллипса, где α — разность фаз колебаний. Если α=mπ (m=0, ±1, ±2, …), эллипс вырождается в отрезок прямой 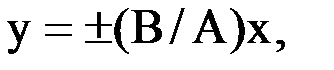 где знак плюс соответствует нулю и четным значениям m, а знак минус — нечетным значениям m. Согласно условию задания, в ответах №2 и №4 α = 0 (четное значениеm). Причем в ответе №2 амплитуды различны, что удовлетворяет форме фигуры В (диагональ прямоугольника).В ответе №4 амплитуды обоих колебаний совпадают, что удовлетворяет форме фигуры D (диагональ квадрата). Если разность фаз α=(2m+1)π/2 (m=0, ±1, ±2, …), уравнение принимает вид:
где знак плюс соответствует нулю и четным значениям m, а знак минус — нечетным значениям m. Согласно условию задания, в ответах №2 и №4 α = 0 (четное значениеm). Причем в ответе №2 амплитуды различны, что удовлетворяет форме фигуры В (диагональ прямоугольника).В ответе №4 амплитуды обоих колебаний совпадают, что удовлетворяет форме фигуры D (диагональ квадрата). Если разность фаз α=(2m+1)π/2 (m=0, ±1, ±2, …), уравнение принимает вид: 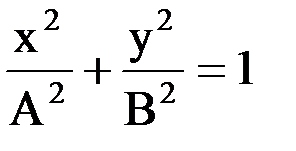 .
. Сопротивление, катушка индуктивности и конденсатор соединены последовательно и включены в цепь переменного тока, изменяющегося по закону
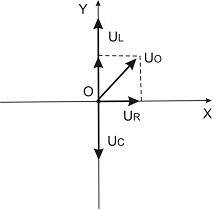
Сопротивление, катушка индуктивности и конденсатор соединены последовательно и включены в цепь переменного тока, изменяющегося по закону  . На рисунке представлена фазовая диаграмма падений напряжения на указанных элементах. Амплитудные значения напряжений соответственно равны: на сопротивлении
. На рисунке представлена фазовая диаграмма падений напряжения на указанных элементах. Амплитудные значения напряжений соответственно равны: на сопротивлении  ; на катушке индуктивности
; на катушке индуктивности  ; на конденсаторе
; на конденсаторе  .
. В) Реактивное сопротивление
В) Реактивное сопротивление . Величина
. Величина 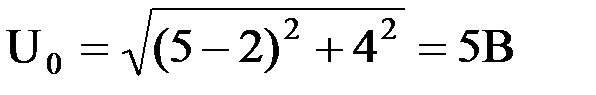 . Полное сопротивление контура найдем по закону Ома:
. Полное сопротивление контура найдем по закону Ома:  , где
, где  ― амплитудные значения напряжения и силы тока. Амплитудное значение силы тока, как это следует из закона его изменения, равно 0,1 А. Тогда полное сопротивление
― амплитудные значения напряжения и силы тока. Амплитудное значение силы тока, как это следует из закона его изменения, равно 0,1 А. Тогда полное сопротивление  . Активное сопротивление
. Активное сопротивление  . Полное сопротивление цепи равно:
. Полное сопротивление цепи равно:  , где
, где  ― реактивное сопротивление;
― реактивное сопротивление;  — индуктивное и емкостное сопротивления соответственно. Отсюда реактивное сопротивление
— индуктивное и емкостное сопротивления соответственно. Отсюда реактивное сопротивление  .
.