
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свободные гармонические колебания и их характеристики
Колебаниями- движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания). Гармонические колебания — колебания при которых колеблющаяся величина изменяется со временем по закону синуса (или косинуса). 1.Уравнение гармонических колебаний:
где х — смещение (отклонение от состояния равновесия) колеблющейся величины, описывающий тот или иной физический процесс; А — амплитуда колебаний; φ — начальная фаза колебаний в момент времени t=0; (ωt+φ) — фаза колебаний в момент времени t; 2. Скорость и ускорение точки, совершающей гармонические колебания:
Пример 14.1 Максимальное значение ускорения точки, совершающей гармонические колебания по закону: £ Решение: ускорение, равное второй производной координаты по времени 3. Энергия гармонических колебаний Кинетическая энергия колеблющейся точки массой m
Потенциальная энергия: Полная энергия гармонического колебания:

Решение: в положенииО пружинный маятник обладает кинетической энергией, потенциальная энергия равна нулю. По закону сохранения энергии кинетическая энергия в положенииО равна потенциальной энергии в положении В. Потенциальную энергию можно найти по формуле
4. Дифференциальное уравнение простейшей колебательной системы (гармонического осциллятора) Гармоническим осциллятором ― называется система, совершающая колебания, описываемые уравнением вида: Пример 14.3. Период колебаний маятника, совершающего свободные колебания, которые описываются дифференциальным уравнением: Решение: дифференциальное уравнение свободных колебаний имеет вид
Гармонические осцилляторы Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур (для токов и напряжений столь малых, что элементы контура модно было бы считать линейными). Пружинный маятник —это груз массой m, подвешенный на обсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы из которого следует, что пружинный маятник совершает гармонические колебания по закону Пример 14.4.Тело массой m прикрепленное к пружине жесткостью k, может без трения двигаться по горизонтальной поверхности (пружинный маятник).
£ Решение: пружинный маятник совершает гармонические колебания по закону
из которого следует, что физический маятник совершает гармонические колебания по закону Пример 14.5.Однородный стержень длинной l0=30см совершает гармонические колебания около неподвижной горизонтальной оси, проходящей конец стержня. Определить приведенную длину L колебаний данного физического маятника. £ Решение: период колебаний физического маятника
Математический маятник ― это идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Уравнение движения маятника, при малых углах его отклонения от положения равновесия, имеет вид:
из которого следует, что физический маятник совершает гармонические колебания по закону Пример 14.6. На рисунках изображены зависимости от времени скорости и ускорения материальной точки, колеблющейся по гармоническому закону.
Циклическая частота колебаний точки равна … £ Решение: амплитудные значение скорости и ускорения определяются по формулам
Колебательный контур -цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостьюС и резистора сопротивлением R. Уравнение свободных гармонических колебаний заряда в контуре, имеет вид:
из которого следует, что заряд Q совершает гармонические колебания по закону где U — напряжение между обкладками конденсатора; I – сила тока. Пример 14.7. Если в колебательном контуре индуктивность катушки увеличить в 2 раза, то период колебаний … £увеличится в 2 раза£уменьшится в 2 разаRувеличится в Решение: в колебательном контуре, состоящем из катушки индуктивности и конденсатора, период собственных колебаний равен Пример 14.8. Электрический колебательный контур радиоприемника настроен на длину волны λ. Как изменятся характеристики процесса колебаний в контуре, если расстояние между пластинами плоского конденсатора увеличить? Установите соответствие между физическими величинами и характером их изменения. А) период колебаний В) собственная частота колебаний С) длина волны Вувеличится А,Суменьшится £ не изменится Решение: емкость плоского конденсатора определяется соотношением Пример 14.9. Напряжение на клеммах конденсатора в колебательном контуре меняется с течением времени согласно графику на рисунке. Какое преобразование энергии происходит в контуре в промежутке от 2×10-3с до 3×10-3 с?
£ энергия магнитного поля катушки преобразуется в энергию электрического поля конденсатора R энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки £ энергия электрического поля конденсатора увеличивается до максимального значения Решение: рассмотрим свободные электромагнитные колебания — колебания, происходящие в идеальном колебательном контуре за счет расходования сообщенной этому контуру энергии, которая в дальнейшем не пополняется. Рисунок иллюстрирует характерные стадии колебаний в контуре за один период.
Отсчет времени t производится с момента подключения к контуру заряженного конденсатора. В первую четверть периода (промежутке времени от 0 доТ/4 ) конденсатор, разряжаясь, создает через контур ток I, идущий по часовой стрелке, и энергия электростатического поля конденсатора превращается в энергию магнитного поля катушки. Во вторую четверть периода (промежутке времени отТ/4 до Т/2) конденсатор перезаряжается и магнитного поля катушки превращается в энергию электрического поля конденсатора. В третью четверть периода (промежутке времени отТ/2 до 3Т/4) конденсатор вновь разряжается и энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки. В последнюю четверть периода (в промежутке времени от 3Т/4 до Т) сила тока в контуре уменьшается, а возникшая в катушке ЭДС самоиндукции препятствует этому. Следовательно, магнитная энергия превращается в электрическую энергию. Согласно графику задания промежуток времени от 2•10-3 с до 3•10-3 с является третьей четвертью периода колебания контура. Значит: на этом участке энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки. |
||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 701. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
, ― круговая (циклическая) частота;
― круговая (циклическая) частота;  — линейнаячастота.
— линейнаячастота.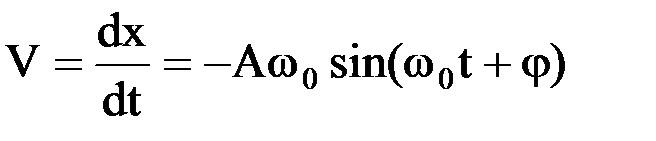 ;
;  .
. , равно …
, равно …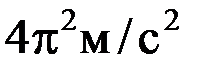 R
R  £
£  £
£ 
 , также меняется по гармоническому закону. Ускорение материальной точки будет максимальным по величине, если
, также меняется по гармоническому закону. Ускорение материальной точки будет максимальным по величине, если 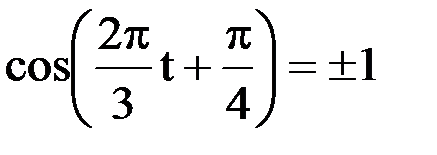 . Амплитуда ускорения равна
. Амплитуда ускорения равна  (в соответствии с общей формулой
(в соответствии с общей формулой  . Следовательно, максимальное значение ускорения равно
. Следовательно, максимальное значение ускорения равно 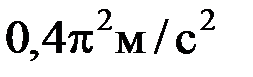 .
. .
.


 Пример 14.2. Шарик, прикрепленный к пружине (пружинный маятник) и насаженный на горизонтальную направляющую, совершает гармонические колебания.На графике представлена зависимость проекции силы упругости пружины на положительное направление оси Х от координаты шарика.В положении О энергия пружинного маятника (в мДж) равна … £ 80 £ 2 R 40 £ 400
Пример 14.2. Шарик, прикрепленный к пружине (пружинный маятник) и насаженный на горизонтальную направляющую, совершает гармонические колебания.На графике представлена зависимость проекции силы упругости пружины на положительное направление оси Х от координаты шарика.В положении О энергия пружинного маятника (в мДж) равна … £ 80 £ 2 R 40 £ 400 , где k ― коэффициент жесткости пружины, х- растяжение (сжатие) пружины. Жесткость пружины можно определить, используя график:
, где k ― коэффициент жесткости пружины, х- растяжение (сжатие) пружины. Жесткость пружины можно определить, используя график:  ;
; 
 . Величину растяжения пружины в положенииВ также можно определить из графика:
. Величину растяжения пружины в положенииВ также можно определить из графика: 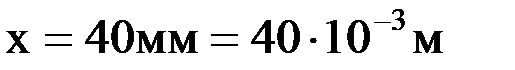 .
.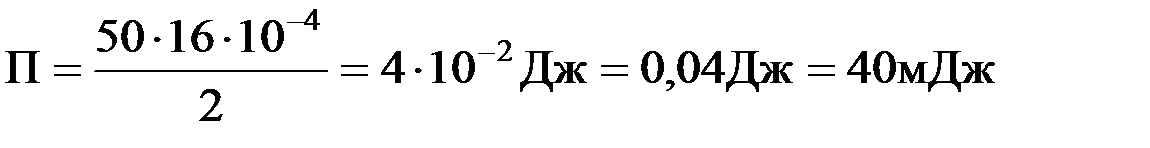 .Следовательно, кинетическая энергия в положенииО равна: К = 40мДж
.Следовательно, кинетическая энергия в положенииО равна: К = 40мДж .
.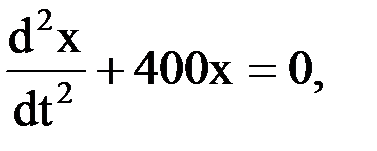 равен …£
равен …£  £
£  £
£  R
R 
 где
где 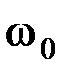 — собственная круговая частота колебаний, которая равна
— собственная круговая частота колебаний, которая равна  . Период колебаний
. Период колебаний 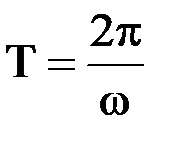 . В данной задаче
. В данной задаче  .
. , где k ― жесткость пружины. Уравнение движения маятника:
, где k ― жесткость пружины. Уравнение движения маятника: 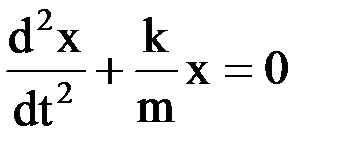 ,
, с циклической частотой
с циклической частотой 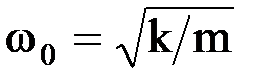 и периодом
и периодом 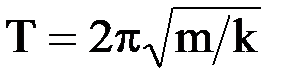 .
.  ЕслиА — амплитуда, то при смещении тела из положения равновесия на величинуx=A/2 скорость тела составит …
ЕслиА — амплитуда, то при смещении тела из положения равновесия на величинуx=A/2 скорость тела составит … £
£  £
£ 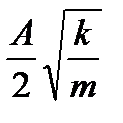 R
R 
 с циклической частотой
с циклической частотой  . Когда тело смещается на величину
. Когда тело смещается на величину  , справедливы соотношения:
, справедливы соотношения:  и
и  , а фаза колебаний
, а фаза колебаний  — равна 60º. Тогда скорость:
— равна 60º. Тогда скорость:  Физический маятник — это твердое тело. Совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точкуО, не совпадающую с центром масс С тела. Уравнение движения маятника, при малых углах его отклонения из положения равновесия, имеет вид:
Физический маятник — это твердое тело. Совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точкуО, не совпадающую с центром масс С тела. Уравнение движения маятника, при малых углах его отклонения из положения равновесия, имеет вид: ,
,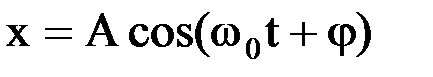 с циклической частотой
с циклической частотой  и периодом
и периодом  , гдеJ― момент инерции маятника относительно оси колебаний; l — расстояние от центра масс маятника до оси колебания;
, гдеJ― момент инерции маятника относительно оси колебаний; l — расстояние от центра масс маятника до оси колебания;  — приведённая длина физического маятника.
— приведённая длина физического маятника. R
R  £
£  £
£ 
 , где l — расстояние центра тяжести маятника от точки подвеса, в данном случае l=l0/2. Момент инерции стержня длиной l0 и массой m относительно оси, проходящей перпендикулярно через конец стержня
, где l — расстояние центра тяжести маятника от точки подвеса, в данном случае l=l0/2. Момент инерции стержня длиной l0 и массой m относительно оси, проходящей перпендикулярно через конец стержня  . Отсюда, подставив выражение для J в выражение для T, получаем
. Отсюда, подставив выражение для J в выражение для T, получаем  . Приведенная длина физического маятника L такова, что период колебаний математического маятника длиной L равен периоду колебаний физического маятника. Поэтому длина приведенная L может быть найдена из уравнения
. Приведенная длина физического маятника L такова, что период колебаний математического маятника длиной L равен периоду колебаний физического маятника. Поэтому длина приведенная L может быть найдена из уравнения 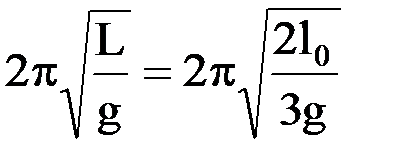 . Отсюда:
. Отсюда:  .
.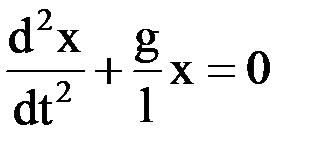 ,
,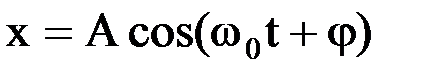 с циклической частотой
с циклической частотой  и периодом
и периодом  , где; l — длина маятника.
, где; l — длина маятника.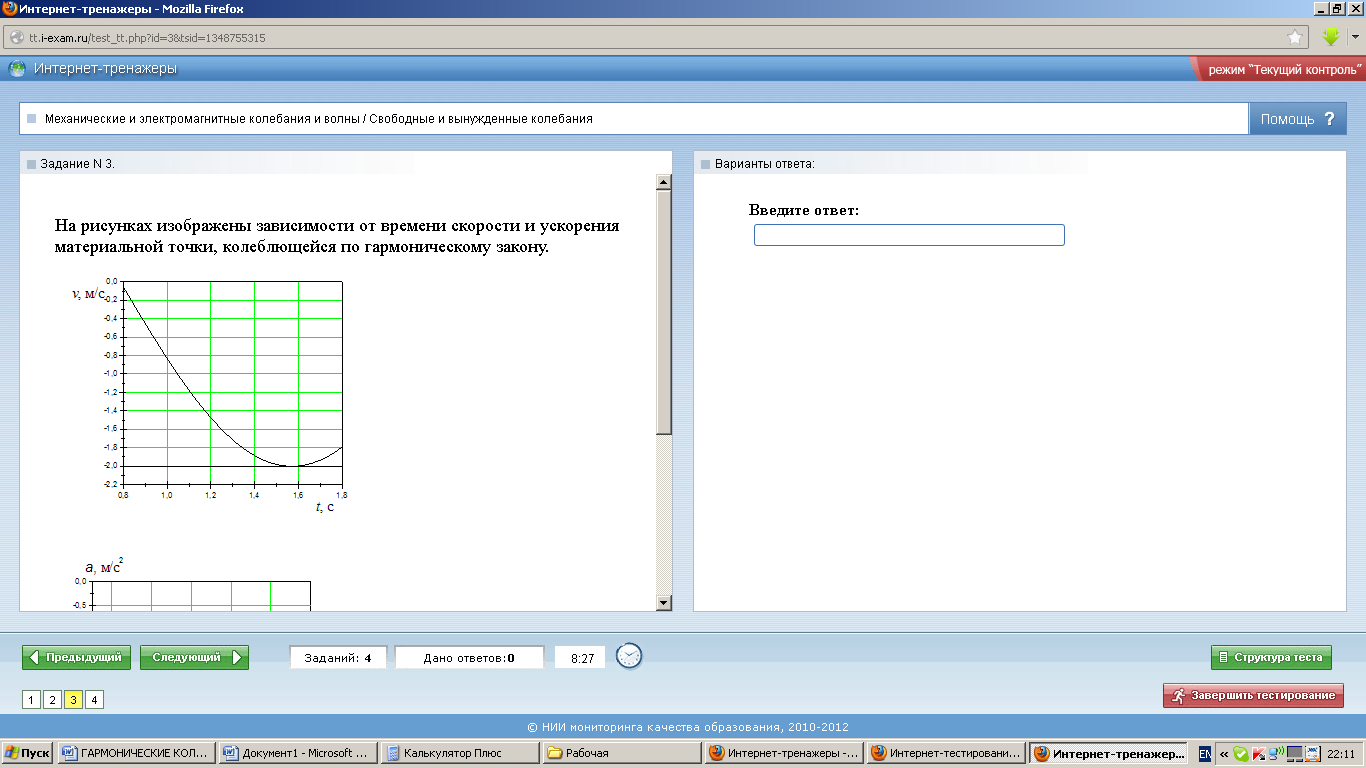

 £
£  R
R  £
£ 
 и
и  соответственно, гдеА — амплитуда координаты (максимальное смещение материальной точки), ω0 ― циклическая частота. Используя графики, находим:
соответственно, гдеА — амплитуда координаты (максимальное смещение материальной точки), ω0 ― циклическая частота. Используя графики, находим:  и
и  . Следовательно,
. Следовательно,  .
.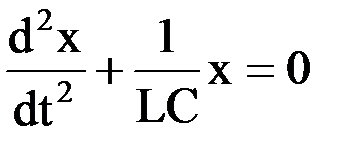 ,
, , где Qmax ― амплитуда колебание заряда с циклической частотой
, где Qmax ― амплитуда колебание заряда с циклической частотой  , называемой собственной частотой контура, и периодом
, называемой собственной частотой контура, и периодом  . Энергия колебательного контура:
. Энергия колебательного контура:  ,
, раза£уменьшится в
раза£уменьшится в  раза
раза , где L — индуктивность катушки, С ― емкость конденсатора. Следовательно, при увеличении индуктивности катушки в 2 раза период колебаний возрастет в
, где L — индуктивность катушки, С ― емкость конденсатора. Следовательно, при увеличении индуктивности катушки в 2 раза период колебаний возрастет в  , где
, где  ― электрическая постоянная, e— диэлектрическая проницаемость среды, S ― площадь пластин конденсатора, расположенных на расстоянии d друг от друга. Согласно условию задания расстояние d между пластинами плоского конденсатора увеличили, следовательно: емкость конденсатора уменьшится. Период собственных колебаний контура равен
― электрическая постоянная, e— диэлектрическая проницаемость среды, S ― площадь пластин конденсатора, расположенных на расстоянии d друг от друга. Согласно условию задания расстояние d между пластинами плоского конденсатора увеличили, следовательно: емкость конденсатора уменьшится. Период собственных колебаний контура равен  , где L — индуктивность катушки, С ― емкость конденсатора. При уменьшении емкости период колебаний тоже уменьшится. Собственная частота колебаний контура
, где L — индуктивность катушки, С ― емкость конденсатора. При уменьшении емкости период колебаний тоже уменьшится. Собственная частота колебаний контура  связана с емкостью конденсатора соотношением
связана с емкостью конденсатора соотношением  , поэтому при уменьшении емкости собственная частота колебаний увеличивается. Период колебаний прямо пропорционален длине волны
, поэтому при уменьшении емкости собственная частота колебаний увеличивается. Период колебаний прямо пропорционален длине волны  и при уменьшении периода, длина волны уменьшится.
и при уменьшении периода, длина волны уменьшится. £ энергия магнитного поля катушки уменьшается от максимального значения до 0
£ энергия магнитного поля катушки уменьшается от максимального значения до 0