
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Исследование формы и расположения гиперболы по ее каноническому видуПоворот гиперболы Парабола Исследование формы и расположения параболы по ее каноническому виду Парабола со смещенной вершиной. Исследование квадратного трехчлена Цели занятия:изучить свойства гиперболы и параболы; на примере лекции 11 найти аналогии в изучении кривых второго порядка; систематизировать знания по теме «Кривые второго порядка»; расширить школьные знания о гиперболе и параболе. Роль и место лекции Школьные представления о гиперболе и параболе ограничены частными случаями параболы ( 1. Гипербола. Определение 1.
Зададим в декартовой системе координат фокусы F1и F2(рис. 1). Возьмем произвольную точку M(x,y), которая по определению должна принадлежать гиперболе. Проведем отрезки F1M и F2M (рис. 1). Согласно определению рассмотрим разность этих отрезков
где
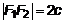 , тогда из , тогда из 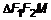 => =>  => =>  или или  . Фокусы имеют координаты . Фокусы имеют координаты 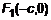 и и 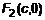 , причем , причем 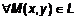 – гипербола. Представим выражение (1) в координатах: – гипербола. Представим выражение (1) в координатах:
Перенесем второе слагаемое в правую часть и возведем обе части равенства в квадрат:
Раскроем скобки и сократим одинаковые члены равенства в левой и правой частях: 
Возведем обе части равенства в квадрат:
Раскроем скобки и сократим одинаковые члены равенства в левой и правой частях:
Перенесем слагаемые с x и y в правую часть, остальные в левую. Вынесем за скобки x2и a2:
Отметим, что
Выражение (3) есть уравнение гиперболы в каноническом виде.
1. Так как текущие координаты входят в уравнение только в квадратах, то гипербола симметрична относительно осей начала координат. Ось симметрии, на которой находятся фокусы гиперболы, называется фокальной осью. 2. Гипербола L (3) пересекается с осями координат: a) Пересечение с осью
б) Пересечение с осью
3. Из уравнения (3) найдем y :
Для I четверти выражение (4) имеет вид 4. Крутизна. Через
 , ,  => =>  , ,
то есть с увеличением x гипербола никогда не пересечет эти прямые, при этом бесконечно приближаясь к ним. Следовательно, l1и l2 – асимптоты гиперболы. 5. Эксцентриситет гиперболы аналогичен эллипсу
Из (5) следует, что 2.1. Частные случаи 1. Если F1 и F2
Причем 2. Если центр гиперболы лежит не в начале координат, а в точке
3. Поворот гиперболы Примем
Повернем систему координат по часовой стрелке на угол
  . (8) . (8)
С учетом
Подставим (9) в (3). Тогда выражение гиперболы в новой системе (повернутой) координат примет вид
Выражение (10) есть уравнение равносторонней гиперболы, осями симметрии которой являются асимптоты. Признаки гиперболы: - коэффициенты при квадратах имеют противоположные знаки; - гипербола пересекает ось координат, одноименную с переменной в квадрате, при которой коэффициент имеет знак «-»; - в случае поворота координатных осей в уравнении кривой второго порядка (см. Лекцию 11) появляются слагаемые произведения переменных. 4. Парабола Определение 2. Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
 – параметр параболы. Проведем прямую d таким образом, чтобы она перпендикулярно пересекала ось – параметр параболы. Проведем прямую d таким образом, чтобы она перпендикулярно пересекала ось  в точке в точке  . Возьмем произвольную точку M(x, y), которая по определению должна принадлежать параболе. Проведем перпендикуляр из этой точки на прямую d. Обозначим точку их пересечения . Возьмем произвольную точку M(x, y), которая по определению должна принадлежать параболе. Проведем перпендикуляр из этой точки на прямую d. Обозначим точку их пересечения  . Согласно определению рассмотрим длины отрезков . Согласно определению рассмотрим длины отрезков  и и  . .
Раскроем скобки и сократим одинаковые члены
Формула (11) – каноническое уравнение параболы 5. Исследование формы и расположения параболы по ее каноническому виду 1. Характерный признак параболы: одна текущая координата в квадрате, а другая в первой степени. 2. Поскольку 3. Найдем точки пересечения уравнения параболы с координатными осями. Пересечение с осью
4. Замечание!!! Если F Вид параболы для различных уравнений
Исследование квадратного трехчлена Задан квадратный трехчлен
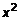 ). Поскольку одна переменная в квадрате, а другая в первой степени, то очевидно, что это парабола (обратное утверждение не верно рис.6). Выделим полные квадраты ). Поскольку одна переменная в квадрате, а другая в первой степени, то очевидно, что это парабола (обратное утверждение не верно рис.6). Выделим полные квадраты
Обозначим
 . (15) . (15)
Это парабола со смещенной вершиной в точку ПРИМЕР 1:
Приведем это уравнение к виду (15): Заключение В лекции изучены понятия «гипербола» и «парабола» в общем виде, построение графиков этих функций. По общему виду уравнения второго порядка можно судить о виде кривой. Отметим следующее: - параметры a и b в выражениях (3, 6, 7) определяют основной прямоугольник гиперболы и следовательно ее асимптоты; - эксцентриситет гиперболы > 1; - эксцентриситет гиперболы определяет ее вытянутость; - при поворотах кривых второго порядка в их общих уравнениях появляются слагаемые произведения текущих переменных; - чем меньше p, тем она более вытянута парабола, а знак p определяет направление ветвей параболы; - степень переменной определяет ось симметрии параболы. Литература 1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980. 2. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001. 3. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002. 4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989, - 659 с.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 484. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ) и гиперболы (
) и гиперболы ( 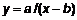 ). Понятия же эти более широкие. В лекции будут рассмотрены такие вопросы как, общее и каноническое уравнения гиперболы и параболы, полученные на основе их классических определений, поворот оси гиперболы, характерные признаки уравнений. Более широко они будут изучаться в теме «Квадратичные формы».
). Понятия же эти более широкие. В лекции будут рассмотрены такие вопросы как, общее и каноническое уравнения гиперболы и параболы, полученные на основе их классических определений, поворот оси гиперболы, характерные признаки уравнений. Более широко они будут изучаться в теме «Квадратичные формы».  Гиперболой называется геометрическое место точек плоскости, разность расстояния которых от двух заданных, называемых фокусами, есть величина постоянная.
Гиперболой называется геометрическое место точек плоскости, разность расстояния которых от двух заданных, называемых фокусами, есть величина постоянная. , (1)
, (1)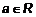 – произвольное число.
– произвольное число.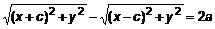 .
. .
.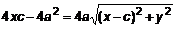 .
.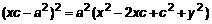 .
.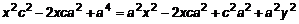 ,
, .
. . (2)
. (2) . Обозначим
. Обозначим 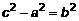 . Запишем выражение (2) через введенные обозначения
. Запишем выражение (2) через введенные обозначения ,
, . (3)
. (3) Рассмотрим выражение (3) и заметим следующее.
Рассмотрим выражение (3) и заметим следующее.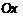 .
. ,
, 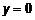 . Из выражения (3) =>
. Из выражения (3) => 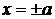 , то есть точки
, то есть точки 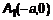 и
и 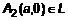 . Эти точки – действительные вершины гиперболы.
. Эти точки – действительные вершины гиперболы.  – действительная ось гиперболы. Отметим эти точки на оси
– действительная ось гиперболы. Отметим эти точки на оси 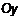 .
.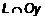 ,
, 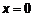 . Из выражения (3) =>
. Из выражения (3) =>  , то есть точек пересечения с осью
, то есть точек пересечения с осью 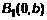 и
и 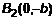 – мнимые вершины гиперболы.
– мнимые вершины гиперболы. 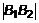 – мнимая ось гиперболы. Отметим эти точки на оси
– мнимая ось гиперболы. Отметим эти точки на оси  . (4)
. (4) (при x=a y=0) значение y увеличивается от 0 до
(при x=a y=0) значение y увеличивается от 0 до  проведем прямые, параллельные осям координат. Получим основной прямоугольник (рис. 2). Через диагонали прямоугольника проведем прямые l1и l2, такие, что
проведем прямые, параллельные осям координат. Получим основной прямоугольник (рис. 2). Через диагонали прямоугольника проведем прямые l1и l2, такие, что  ,
,  . Сравним ординаты l1и координаты гиперболы L в первой четверти при одних и тех же значениях x
. Сравним ординаты l1и координаты гиперболы L в первой четверти при одних и тех же значениях x . (5)
. (5) . Причем, если
. Причем, если 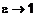 , гипербола вытягивается вдоль оси
, гипербола вытягивается вдоль оси  , гипербола вытягивается вдоль оси
, гипербола вытягивается вдоль оси  , то каноническое уравнение гиперболы принимает вид
, то каноническое уравнение гиперболы принимает вид . (6)
. (6)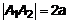 – мнимая ось гиперболы,
– мнимая ось гиперболы, 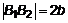 – действительная ось.
– действительная ось.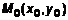 , то уравнение гиперболы (3) примет вид
, то уравнение гиперболы (3) примет вид . (7)
. (7)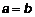 , тогда уравнение гиперболы примет вид
, тогда уравнение гиперболы примет вид .
. (рис. 3). Тогда асимптоты совпадут с координатными осями новой системы координат. Выразим старые координаты
(рис. 3). Тогда асимптоты совпадут с координатными осями новой системы координат. Выразим старые координаты  через новые
через новые 
 ,
,  . (9)
. (9) или
или  . Откуда
. Откуда
 . (10)
. (10)
 .
.
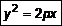 . (11)
. (11)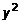 , то парабола симметрична относительно оси
, то парабола симметрична относительно оси  – вершина параболы, единственная точка пересечения с координатными осями.
– вершина параболы, единственная точка пересечения с координатными осями. Построим параболу. Для этого из (11) выразим
Построим параболу. Для этого из (11) выразим  . Для первой четверти это выражение примет вид
. Для первой четверти это выражение примет вид  . При увеличении x от 0 до
. При увеличении x от 0 до  (при x=0 y=0) значение y увеличивается от 0 до
(при x=0 y=0) значение y увеличивается от 0 до  . (12)
. (12)
 6. Парабола со смещенной вершиной
6. Парабола со смещенной вершиной . (13)
. (13)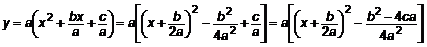
 . (14)
. (14)
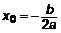 ,
, 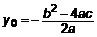 ,
,  . Тогда выражение (14) запишем в виде
. Тогда выражение (14) запишем в виде .
. Построить кривую, определяемую уравнением
Построить кривую, определяемую уравнением  .
. ,
,  – это парабола вида (рис.5) с вершиной в точке (-4,-1) и ветвями, повернутыми влево (т.к.
– это парабола вида (рис.5) с вершиной в точке (-4,-1) и ветвями, повернутыми влево (т.к.  ). Ось симметрии параллельна оси
). Ось симметрии параллельна оси  Поверхности второго порядка
Поверхности второго порядка