Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
КлассификациянапряженныхсостоянийИз уравнений (37) ... (41) можно исключить перерезывающие силы Рассмотрим метод упрощения уравнений моментной теории оболочек,основанный на малости толщины оболочки по сравнению с ее радиусами кривизны. Средние по толщине оболочки напряжения можно определить из уравнений (31) ... (33):
Моментные (изгибные) напряжения при
В этих формулах величина Рассмотрим структуру выражений для деформаций
Эти выражения не зависят от толщины hоболочки. Рассмотрим условия влияния кривизны оболочки. Пусть

Так как величина h/(2RQ)мала, то на первый взгляд из формул (46) следует парадоксальный вывод, что все слагаемые с изменениями кривизны можно отбросить. Но в этом случае напряжения будут определяться только деформациями Более глубокий анализ показывает, что величины Но дифференцирование функции может увеличить порядок ее величины, т. е. максимальное значение производной может быть больше максимального значения самой функции. Порядок абсолютного значения какой-либо функции можно обозначить введением фигурных скобок. Например, порядок величины wобозначается{
где
Из этих формул следует
Если
Из этого простого анализа следуют три важных вывода. 1. Напряженное состояние моментной оболочки, описываемое функциями с малой изменяемостью, т. е. функциями, порядок которых не возрастает при дифференцировании, можно приближенжгнай-ти^'по безмоментной теории оболочек, полагая 2.Если средние напряжения от сил 3. Если изгибные напряжения значительно больше средних напряжений от сил
Это напряжённое состояние соответствует деформированию оболочки без растяжения и сдвига средней поверхности. В общей теории тонких оболочек первое напряжённое состояние называется безмоментным, второе смешанным, третье моментным.
Краевой эффект. В случае осесимметричной деформации положим Полная система уравнений будет иметь вид:
Если нагрузки Рассмотрим однородные уравнения, когда
где Будем также считать, что величина Положим, что
Из этих уравнений следует, что
Из соотношения (51) с той же точностью следует
Уравнения равновесия (52) и (53) сразу упростить нельзя, так как неизвестен относительный порядок величин
Умножив последнее уравнение на
Константа соответствующая продольной силе
Уравнение для краевого эффекта примет вид
Сравним порядки величин меридионального и окружного усилий в краевой зоне.
Следовательно получим
Подставив эту зависимость в выражение (59), получим
Обозначим
Для сферической оболочки При k=constполучаем
Где A,B,Cи D - произвольные константы. Выражение (61) обладает тем свойством, что при каждом дифференцировании оно возрастает в kраз:
Следовательно, это решение удовлетворяет условию малости функции по сравнению с производной. Рассмотрим затухающую часть выражения (61):
Величины
Рассмотрим последовательность расчета осесимметрично нагруженной оболочки вращения по моментной теории с разделением напряженного состояния на безмоментное и краевой эффект. Сначала по безмоментной теории определяют силы ТъТ2и перемещения и,wпо заданным внешним нагрузкам и граничным условиям для величины Тхили и.(В выражение для перемещений может входить константа интегрирования, соответствующая перемещению оболочки как твердого тела.) Затем, решая однородные уравнения краевого эффекта для каждого торца, находят общие выражения для величин е2, ЪХУМги Qxчерез соответствующие константы интегрирования (по две константы на каждом торце). Наконец, составляют граничные условия для каждого торца оболочки. Если заданы силовые граничные условия, т. е. величины Мг и Ql9то сразу определяют константы интегрирования уравнений краевого эффекта. Если заданы геометрические условия, т. е. величины s2 и то по значениям перемещений ииwбезмоментного решения определяют величины е2о и OlQ(перемещение оболочки как твердого тела в них не войдет) и составляют суммарные выражения для е2 и $г от безмоментного решения и краевого эффекта. Константы интегрирования, входящие в эти выражения, определяют из заданных геометрических граничных условий.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 452. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
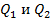 а в оставшиеся уравнения подставить выражения сил Т1, Т2, Sи моментов
а в оставшиеся уравнения подставить выражения сил Т1, Т2, Sи моментов  через перемещения
через перемещения 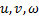 и их производные и получить три дифференциальных уравнения в частных производных для определения перемещений. Однако практическое решение этих уравнений наталкивается на большие математические трудности.
и их производные и получить три дифференциальных уравнения в частных производных для определения перемещений. Однако практическое решение этих уравнений наталкивается на большие математические трудности.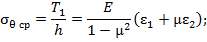
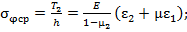 (42)
(42)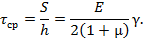
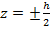 можно определить из уравнений (34)...(36):
можно определить из уравнений (34)...(36):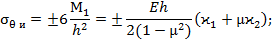
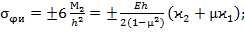 (43)
(43)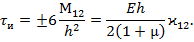
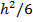 есть погонный момент сопротивления нормальных сечений оболочки, высота которых равна h, а ширина равна единице.
есть погонный момент сопротивления нормальных сечений оболочки, высота которых равна h, а ширина равна единице. и параметров
и параметров 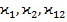 изменений кривизны. Возьмём для определённости выражения
изменений кривизны. Возьмём для определённости выражения 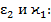
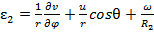 (44)
(44)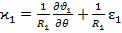 (45)
(45)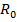 - какой-либо характерный размер срединной поверхности, например радиус кривизны
- какой-либо характерный размер срединной поверхности, например радиус кривизны 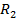 торцевого сечения оболочки. Введём вместо величин
торцевого сечения оболочки. Введём вместо величин 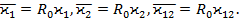 Тогда согласно формулам (42) и (43) суммарные напряжения в оболочке при
Тогда согласно формулам (42) и (43) суммарные напряжения в оболочке при 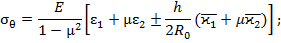
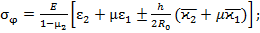 (46)
(46)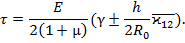
 безмоментного состояния.
безмоментного состояния.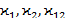 , а следовательно, и
, а следовательно, и 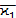 ,
, 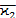 ,
, 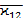 отличаются от величин
отличаются от величин 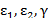 порядками част-
порядками част-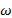 . Так, из рассмотрения формул
. Так, из рассмотрения формул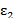 входит толь-
входит толь-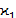 — вторая
— вторая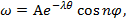
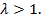 Тогда
Тогда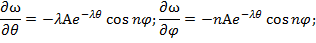
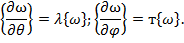
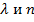 - большие числа, то можно сказать, что дифференцирование функции
- большие числа, то можно сказать, что дифференцирование функции 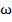 по
по 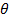 увеличивает её порядок величины в
увеличивает её порядок величины в 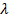 раз, а дифференцирование по
раз, а дифференцирование по 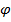 в nраз. В теории оболочек коэффициенты
в nраз. В теории оболочек коэффициенты 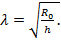 Тогда
Тогда 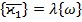 и соответствующими слагаемыми в формулах (46) уже нельзя пренебрегать. В этом случае
и соответствующими слагаемыми в формулах (46) уже нельзя пренебрегать. В этом случае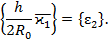
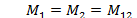
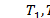 и изгибные напряжения от моментов
и изгибные напряжения от моментов 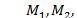 имеют один и тот же порядок, то соответствующее напряженное состояние имеет большой коэффициент изменяемости (в одном или двух направлениях). Его можно определить из общих уравнений теории оболочек, а также приближенных уравнений, учитывающих различные порядки величин производных от перемещений, усилий и моментов.
имеют один и тот же порядок, то соответствующее напряженное состояние имеет большой коэффициент изменяемости (в одном или двух направлениях). Его можно определить из общих уравнений теории оболочек, а также приближенных уравнений, учитывающих различные порядки величин производных от перемещений, усилий и моментов.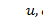 для такого напряженного состояния можно определить из уравнений
для такого напряженного состояния можно определить из уравнений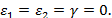
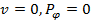 и все величины - не зависящими от угловой координаты
и все величины - не зависящими от угловой координаты 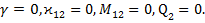
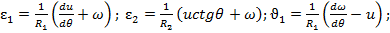 (47)
(47)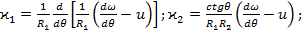 (48)
(48)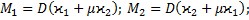 (49)
(49)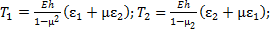 (50)
(50)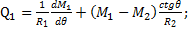 (51)
(51)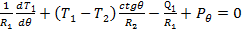 (52)
(52)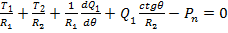 (53)
(53)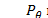 меняются вдоль меридиана достаточно плавно, частное решение уравнений можно, как уже указывалось, найти по формулам безмоментной теории оболочек.
меняются вдоль меридиана достаточно плавно, частное решение уравнений можно, как уже указывалось, найти по формулам безмоментной теории оболочек.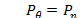 . Моментное напряженное состояние при осесимметричной деформации теряет смысл, так как из решения уравнений
. Моментное напряженное состояние при осесимметричной деформации теряет смысл, так как из решения уравнений 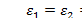 получаются перемещения ииw,соответствующие лишь движению оболочки как твердого тела вдоль оси симметрии. Для приближенного определения смешанного напряженного состояния, которое соответствует краевому эффекту, рассмотрим упрощения исходных уравнений, следующие из условия быстрой изменяемости напряженного состояния вдоль меридиана. Будем считать,-что для всех искомых сил и перемещений выполняется условие
получаются перемещения ииw,соответствующие лишь движению оболочки как твердого тела вдоль оси симметрии. Для приближенного определения смешанного напряженного состояния, которое соответствует краевому эффекту, рассмотрим упрощения исходных уравнений, следующие из условия быстрой изменяемости напряженного состояния вдоль меридиана. Будем считать,-что для всех искомых сил и перемещений выполняется условие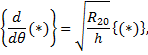
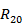 — окружной радиус кривизны у края оболочки.
— окружной радиус кривизны у края оболочки. для любого края оболочки не слишком велика и радиусы кривизны Rl ,R2изменяются вдоль меридиана достаточно плавно. Естественно предположить, что порядок величины перемещения
для любого края оболочки не слишком велика и радиусы кривизны Rl ,R2изменяются вдоль меридиана достаточно плавно. Естественно предположить, что порядок величины перемещения  выше порядка величины перемещения и.
выше порядка величины перемещения и.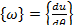 Тогда главные значения величин, определенных формулами (47) и (48), равны:
Тогда главные значения величин, определенных формулами (47) и (48), равны: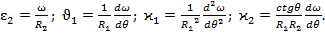 (54)
(54)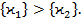 Поэтому можно считать, что
Поэтому можно считать, что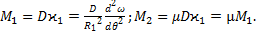 (55)
(55)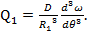 (56)
(56)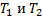 . Исключим из этих двух уравнений величину
. Исключим из этих двух уравнений величину 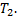 Умножим уравнение (53) на
Умножим уравнение (53) на 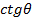 и сложим его с уравнением (52). Так как по условию
и сложим его с уравнением (52). Так как по условию 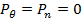 , получим
, получим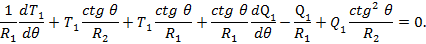
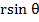 , получим
, получим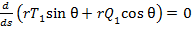 (57)
(57)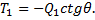 (58)
(58)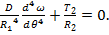 (59)
(59)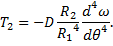
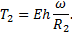
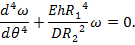
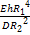 =12(1-
=12(1- 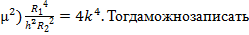
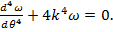 (60)
(60)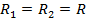 и коэффициент
и коэффициент 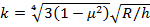 является постоянным большим числом (при
является постоянным большим числом (при 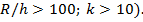
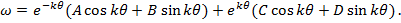 (61)
(61)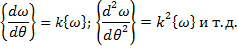
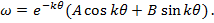
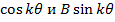 являются периодическими функциями угловой координаты
являются периодическими функциями угловой координаты 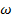 уменьшается в
уменьшается в 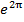 раз, т.е. становится пренебрежимо малой величиной. Длина отрезка меридиана, соответствующая этому периоду, равна
раз, т.е. становится пренебрежимо малой величиной. Длина отрезка меридиана, соответствующая этому периоду, равна