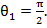Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Осесимметричная задача для безмоментной оболочки.Принимая
выражения деформаций через перемещения:
где
закон Гука с учётом температурного расширения:
Из уравнения (11) окружная сила равна
Подставляя выражение (16) в уравнение (10) и учитывая, что получаем
Примем
Где P=P(s) - новая искомая функция. Подставляя это выражение для
получаем после умножения на
Отсюда
где Тогда,
Следовательно, формула (19) определяет эпюру продольных сил, растягивающих оболочку как стержень переменного сечения. Окружное усилие передаётся из формулы (16)
 Рассмотрим практически нагружение оболочки внутренним давлением. Принимая
при нагружении внутренним давлением
Формулу (22) легко получить непосредственно из теоремы Паскаля, так как
Кольцевое усилие
Для цилиндрической оболочки
Для сферической оболочки
По безмоментной теории оболочек перемещения точек срединной поверхности легко найти из уравнений (12), (13), (16) если известны силы
Вычитая из первого уравнения второе, получаем
где Интегрируя выражение (24), находим
Произвольная константа С соответствует перемещению оболочки как твёрдого тела вдоль оси х. Из уравнения (23) получим
Перемещение в направлении оси вращения оболочки определяется формулой
Для цилиндрических и конических оболочек, где неудобно пользоваться независимой переменной Получим
Отсюда интегрированием определяют перемещение u. Перемещение
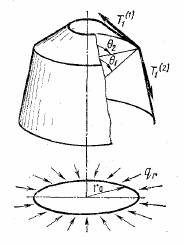
Рассмотрим условия сопряжения двух оболочек вращения на основе безмоментной теории. В месте стыка угол
Проекция этих же сил на плоскость параллели даст погонную нагрузка
Эта нагрузка не может быть воспринята безмоментными оболочками. Стык должен быть усилен достаточно прочным и жестким шпангоутом. Нагрузка Сжимающие усилие в шпангоуте
Например, для шпангоута в стыке цилиндрической оболочки со сферическим днищем, нагруженным равномерным гидростатическим давлением P, имеем |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 481. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
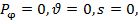 а перемещения
а перемещения 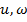 и силы
и силы 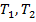 зависящими только от координаты
зависящими только от координаты 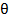 (или s), получаем уравнения равновесия:
(или s), получаем уравнения равновесия: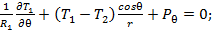 (10)
(10)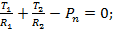 (11)
(11)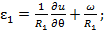 (12)
(12)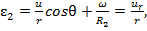 (13)
(13)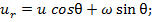
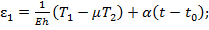 (14)
(14)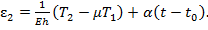 (15)
(15)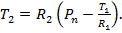 (16)
(16)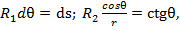
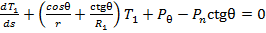 (17)
(17)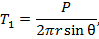
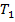 в уравнение (17) и учитывая тождества
в уравнение (17) и учитывая тождества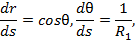
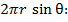
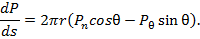
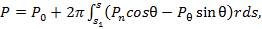 (18)
(18)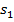 определяет граничное сечение оболочки. Величина
определяет граничное сечение оболочки. Величина 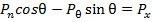 есть проекция нагрузки но ось x.
есть проекция нагрузки но ось x.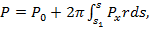 (19)
(19)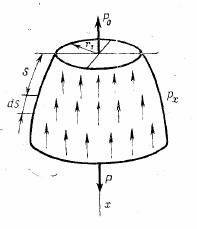
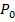 -продольная сила, приложенная в торцевом сечении;
-продольная сила, приложенная в торцевом сечении; 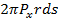 -осевая нагрузка, действующая на элементарное кольцо оболочки длиной ds.
-осевая нагрузка, действующая на элементарное кольцо оболочки длиной ds.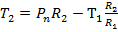 (20)
(20)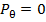 и
и 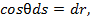 из уравнения (18) получаем
из уравнения (18) получаем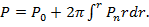 (21)
(21)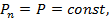 то
то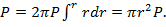 (22)
(22)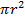 -проекция поверхности оболочки на плоскость, перпендикулярную направлению действия силы Р. В этом случае меридиональное усилие
-проекция поверхности оболочки на плоскость, перпендикулярную направлению действия силы Р. В этом случае меридиональное усилие 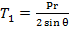 . Но
. Но 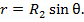 Следовательно
Следовательно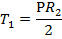
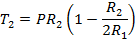
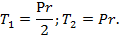
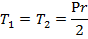
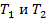
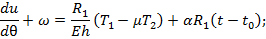
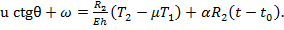 (23)
(23)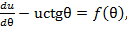 (24)
(24)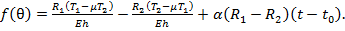
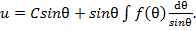 (25)
(25)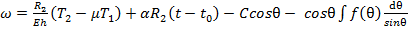 (26)
(26)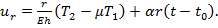 (27)
(27)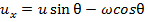 . Тогда получаем
. Тогда получаем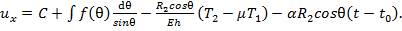 (28)
(28)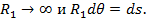
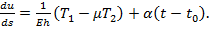 (29)
(29)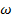 определяют из уравнения (23). Для сферической оболочки
определяют из уравнения (23). Для сферической оболочки 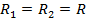 и
и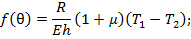
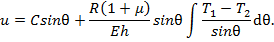
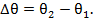
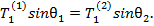
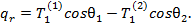
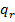 будет расчётной сжимающей нагрузкой для этого шпангоута.
будет расчётной сжимающей нагрузкой для этого шпангоута.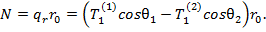
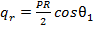 , так как в этом случае
, так как в этом случае 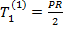 , где R-радиус кривизны днища, а
, где R-радиус кривизны днища, а